108.将有序数组转换为二叉搜索树

题目:108.将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 平衡 二叉搜索树。

• 示例 1：

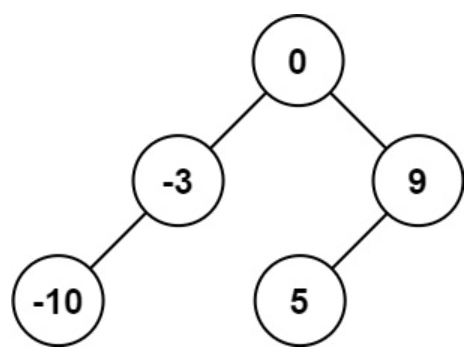
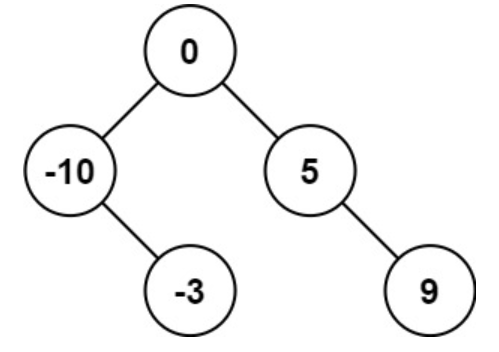
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

• 示例 2：

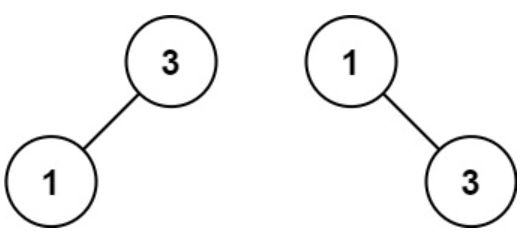
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

• 提示：

1 <= nums.length <= 10^4
-10^4 <= nums[i] <= 10^4
nums 按 严格递增 顺序排列

思路

为了将一个已经按升序排列的整数数组 nums 转换为一棵 平衡二叉搜索树 (BST)，我们可以利用递归的方法。因为数组已经有序，我们可以通过选择中间的元素作为根节点，保证左右子树的节点数量尽量平衡。

1. 数组的中间元素将作为根节点。
2. 左半部分递归构建左子树，右半部分递归构建右子树。
3. 这个过程不断重复，直到数组为空为止。

• 时间复杂度:O(n)
• 时间复杂度:O(log₂n)

代码

public TreeNode sortedArrayToBST(int[] nums) {
    return toBSTHelper(nums, 0, nums.length - 1);
}

// 辅助递归函数，用于将数组的某个区间 [left, right] 转换为BST
private TreeNode toBSTHelper(int[] nums, int left, int right) {
    if (left > right) {
        return null;
    }
    // 选择中间元素作为当前子树的根节点
    int mid = left + (right - left) / 2;
    TreeNode root = new TreeNode(nums[mid]);
    // 递归构建左子树
    root.left = toBSTHelper(nums, left, mid - 1);
    // 递归构建右子树
    root.right = toBSTHelper(nums, mid + 1, right);
    return root;
}