题目:909.蛇梯棋
给你一个大小为 n x n 的整数矩阵 board ,方格按从 1 到 n^2 编号,编号遵循 转行交替方式 ,从左下角开始 (即,从 board[n - 1][0] 开始)的每一行改变方向。
你一开始位于棋盘上的方格 1。每一回合,玩家需要从当前方格 curr 开始出发,按下述要求前进:
- 选定目标方格
next,目标方格的编号在范围[curr + 1, min(curr + 6, n^2)]。
该选择模拟了掷 六面体骰子 的情景,无论棋盘大小如何,玩家最多只能有6个目的地。 - 传送玩家:如果目标方格
next处存在蛇或梯子,那么玩家会传送到蛇或梯子的目的地。否则,玩家传送到目标方格next。 - 当玩家到达编号
n^2的方格时,游戏结束。
如果 board[r][c] != -1 ,位于 r 行 c 列的棋盘格中可能存在 “蛇” 或 “梯子”。那个蛇或梯子的目的地将会是 board[r][c]。编号为 1 和 n^2 的方格不是任何蛇或梯子的起点。
注意,玩家在每回合的前进过程中最多只能爬过蛇或梯子一次:就算目的地是另一条蛇或梯子的起点,玩家也 不能 继续移动。
举个例子,假设棋盘是 [[-1,4],[-1,3]] ,第一次移动,玩家的目标方格是 2 。那么这个玩家将会顺着梯子到达方格 3 ,但 不能 顺着方格 3 上的梯子前往方格 4 。(简单来说,类似飞行棋,玩家掷出骰子点数后移动对应格数,遇到单向的路径(即梯子或蛇)可以直接跳到路径的终点,但如果多个路径首尾相连,也不能连续跳多个路径)
返回达到编号为 n^2 的方格所需的最少移动次数,如果不可能,则返回 -1。
- 示例 1:
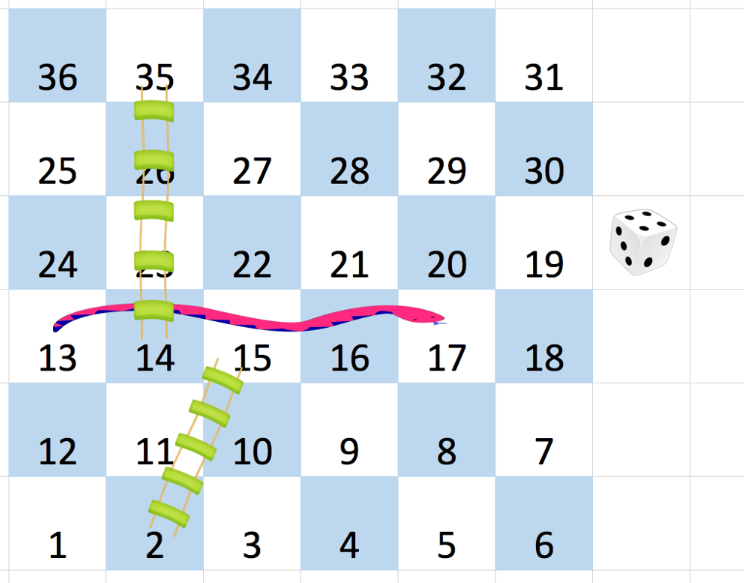
输入:board = [[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,35,-1,-1,13,-1],[-1,-1,-1,-1,-1,-1],[-1,15,-1,-1,-1,-1]]
输出:4
解释:
首先,从方格 1 [第 5 行,第 0 列] 开始。
先决定移动到方格 2 ,并必须爬过梯子移动到到方格 15 。
然后决定移动到方格 17 [第 3 行,第 4 列],必须爬过蛇到方格 13 。
接着决定移动到方格 14 ,且必须通过梯子移动到方格 35 。
最后决定移动到方格 36 , 游戏结束。
可以证明需要至少 4 次移动才能到达最后一个方格,所以答案是 4 。 - 示例 2:
输入:board = [[-1,-1],[-1,3]]
输出:1- 提示:
n == board.length == board[i].length
2 <= n <= 20
board[i][j] 的值是 -1 或在范围 [1, n^2] 内
编号为 1 和 n^2 的方格上没有蛇或梯子思路
解释一下题意
一个n * n的棋盘,起点是左下角,一次可以走 1-6 步
从左下角开始棋盘编号从下往上蛇形递增
7 8 9
6 5 4
1 2 3
如上图所示:
起点是 1,终点是 9(n * n) (1-9为棋盘编号)
每格棋盘单元格内容一般是 -1
如果棋盘单元格内容不是 -1,而是一个数字,
则如果跳到这里,就要传送到指定数字编号的棋盘单元格中
-1 -1 -1
-1 -1 -1
-1 -1 8
如图:走到第三个格的位置,就会自动被传送到 8 的位置注意:如果传送到的棋盘单元格内容也不是 -1,无法进行 二次传送。
将二维棋盘转化为一维数组,取最下方为第一行,奇数行正向,偶数行反向,从下往上之字形遍历。
广度优先搜索找到起点到终点的最短路径 (如果走到需要传送的位置,则移动到目标位置)。
时间复杂度:O(n²)
时间复杂度:O(n²)
代码
public int snakesAndLadders(int[][] board) {
int result = 0;
int[] nums = twoToOne(board);
Queue<Integer> queue = new ArrayDeque<>();
// 存储已经遍历过的位置
Set<Integer> visited = new HashSet<>();
// 从第一个格子开始
queue.offer(0);
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
int current = queue.poll();
// 如果到达了最后一个格子,返回步数
if (current == nums.length - 1) {
return result;
}
if (!visited.contains(current)) {
// 将当前位置标记为已访问
visited.add(current);
// 掷骰子,向前最多移动6格,不能走出棋盘
for (int step = 1; step <= 6 && (current + step) < nums.length; step++) {
int next = current + step;
if (nums[next] == -1) {
queue.offer(next);
} else {
// 如果走到需要传送的位置,则移动到目标位置(将目标位置坐标添加进队列)
queue.offer(nums[next] - 1);
}
}
}
}
result++;
}
return -1;
}
// 将二维棋盘转化为一维数组
private int[] twoToOne(int[][] board) {
int n = board.length;
int[] nums = new int[n * n];
int count = 0;
for (int i = n - 1; i >= 0; i--) {
//取最下方为第一行,奇数行正向,偶数行反向
int row = n - i;
if (row % 2 != 0) {
for (int j = 0; j < n; j++) {
// 从左向右遍历
nums[count++] = board[i][j];
}
} else {
for (int j = n - 1; j >= 0; j--) {
// 从右向左遍历
nums[count++] = board[i][j];
}
}
}
return nums;
}
