230.二叉搜索树中第 K 小的元素

题目:230.二叉搜索树中第 K 小的元素

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（从 1 开始计数）。

• 示例 1：

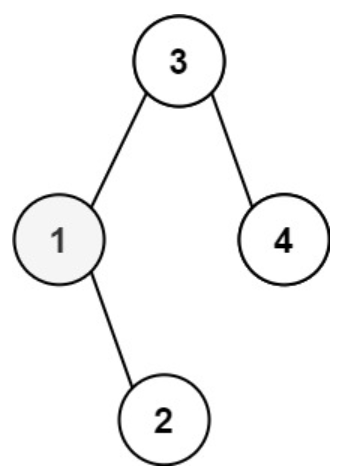
输入：root = [3,1,4,null,2], k = 1
输出：1

• 示例 2：

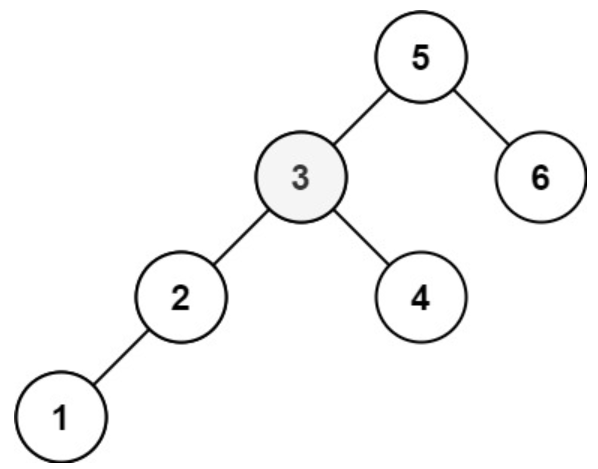
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

• 提示：

树中的节点数为 n 。
1 <= k <= n <= 10^4
0 <= Node.val <= 10^4

• 进阶：

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

思路

要在二叉搜索树 (BST) 中找到第 k 小的元素，可以利用 BST 的性质：中序遍历会得到一个递增的序列。我们可以使用中序遍历来找到第 k 小的元素。

1. 中序遍历：对 BST 进行中序遍历，在遍历过程中维护一个计数器，记录当前已访问节点的数量。
2. 查找第 k 小元素：当计数器等于 k 时，当前遍历到的节点就是第 k 小的元素，返回该节点的值。

• 时间复杂度:O(h+k)，其中 h 是二叉树的高度
• 空间复杂度:O(h)，其中 h 是二叉树的高度

代码

class Solution {
    private int count = 1;
    private int num = 0;

    public int kthSmallest(TreeNode root, int k) {
        inorderTraversal(root, k);
        return this.num;
    }

    private void inorderTraversal(TreeNode node, int k) {
        if (node == null) {
            return;
        }
        inorderTraversal(node.left, k);
        // 当计数器等于 k 时，当前遍历到的节点就是第 k 小的元素
        if (this.count == k) {
            this.num = node.val;
        }
        this.count++;
        inorderTraversal(node.right, k);
    }
}