222.完全二叉树的节点个数

题目:222.完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1 ~ 2^h 个节点。

• 示例 1：

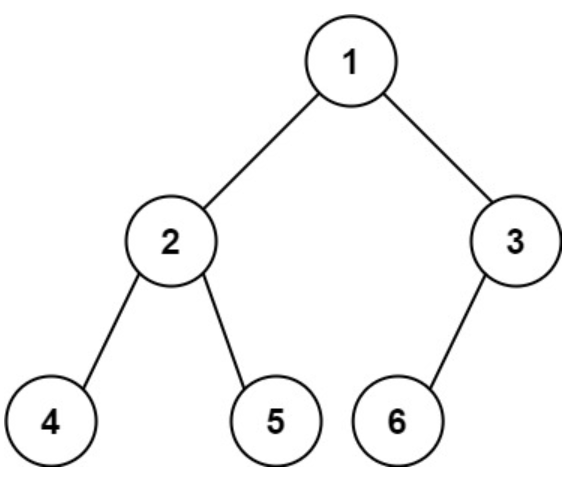
输入：root = [1,2,3,4,5,6]
输出：6

• 示例 2：

输入：root = []
输出：0

• 示例 3：

输入：root = [1]
输出：1

• 提示：

树中节点的数目范围是[0, 5 * 10^4]
0 <= Node.val <= 5 * 10^4
题目数据保证输入的树是 完全二叉树

• 进阶：

进阶：遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

思路1

中序遍历完全二叉树来统计节点

• 时间复杂度:O(n)，其中 n 是二叉树的节点数
• 空间复杂度:O(h)，其中 h 是二叉树的高度

代码

public int countNodes(TreeNode root) {
    // 定义一个数组，方便在方法内修改节点数的值
    int[] countArray = new int[1];
    inorderTraversal(root, countArray);
    return countArray[0];
}

private void inorderTraversal(TreeNode root, int[] countArray) {
    if (root == null) {
        return;
    }
    inorderTraversal(root.left, countArray);
    countArray[0]++;
    inorderTraversal(root.right, countArray);
}

思路2

要计算完全二叉树的节点个数，可以利用完全二叉树的性质，通过高度的计算来减少不必要的遍历，从而在平均情况下降低时间复杂度。

1. 完全二叉树的特性：

   • 完全二叉树的所有层都是满的，除了可能是最底层。
   • 如果树的高度为 h，则最大节点数为 2^h − 1。
   • 利用左右子树的高度来确定左右子树是否为满二叉树。

2. 算法步骤：

   • 计算左子树和右子树的高度。
   • 如果左右子树的高度相等，则左子树为满二叉树，节点数为 2^leftHeight − 1，加上根节点，再递归计算右子树的节点数。
   • 如果高度不相等，右子树为满二叉树，节点数为 2^rightHeight − 1，加上根节点，再递归计算左子树的节点数。

• 时间复杂度:O(log₂(n))
• 空间复杂度:O(log₂(n))

代码

public int countNodes(TreeNode root) {
    if (root == null) {
        return 0;
    }
    int leftHeight = countHeight(root.left);
    int rightHeight = countHeight(root.right);
    if (leftHeight == rightHeight) {
        // 左子树是满的，节点数为 2^leftHeight - 1，加上根节点和右子树的节点
        // 1 << n: 表示将数字 1 向左移动 n 位
        return (1 << leftHeight) + countNodes(root.right);
    } else {
        // 右子树是满的，节点数为 2^rightHeight - 1，加上根节点和左子树的节点
        return (1 << rightHeight) + countNodes(root.left);
    }
}