106.从中序与后序遍历序列构造二叉树

题目:106.从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

• 示例 1：

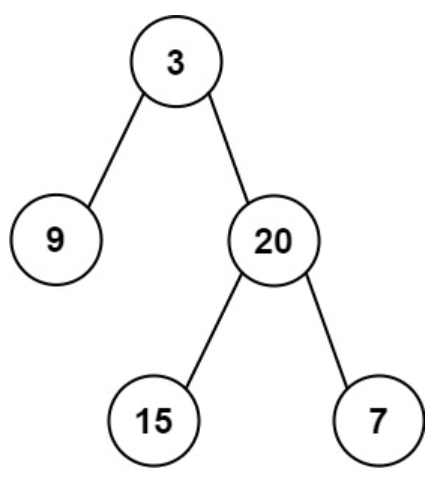
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

• 示例 2：

输入：inorder = [-1], postorder = [-1]
输出：[-1]

• 提示：

1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由 不同 的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历

思路

构造二叉树时可以递归地构造树的左子树和右子树。利用中序遍历 (inorder) 和后序遍历 (postorder) 的性质。后序遍历的最后一个节点是树的根节点，通过该根节点将中序遍历划分为左子树和右子树，再递归构造子树。

1. 后序遍历的特点：

   • 最后一个元素是根节点。

2. 中序遍历的特点：

   • 根节点左边的部分是左子树，右边的部分是右子树。

3. 构造过程：

   • 从后序遍历中取出根节点。
   • 在中序遍历中找到根节点的位置，划分出左子树和右子树。
   • 递归地构造左子树和右子树。

4. 以示例1为例：
   

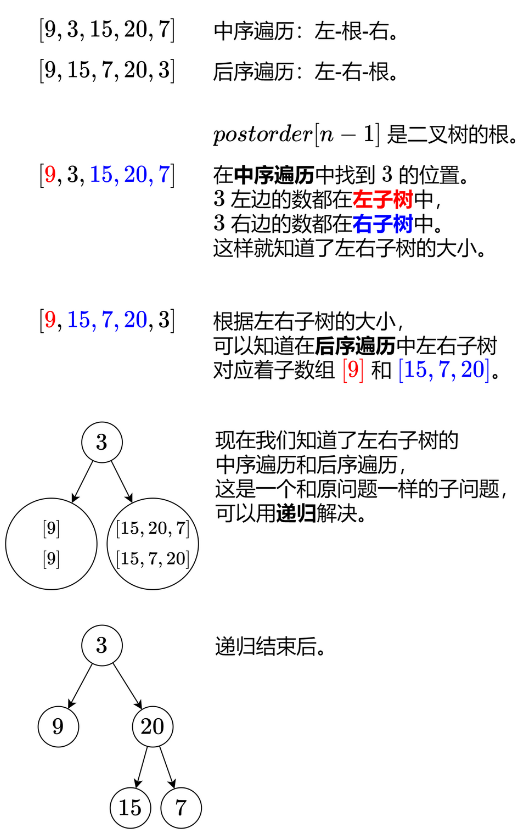
• 时间复杂度:O(n²)
• 空间复杂度:O(n)

代码

public TreeNode buildTree(int[] inorder, int[] postorder) {
    int n = inorder.length;
    if (n == 0) {
        return null;
    }
    int root = postorder[n - 1];
    // 左子树的大小
    int leftSubTreeSize = 0;
    // 找到 root 在 inorder 中的下标
    for (int i = 0; i < n; i++) {
        if (root == inorder[i]) {
            leftSubTreeSize = i;
        }
    }
    // 左子树的中序遍历
    int[] leftSubTreeInorder = Arrays.copyOfRange(inorder, 0, leftSubTreeSize);
    // 右子树的中序遍历
    int[] rightSubTreeInorder = Arrays.copyOfRange(inorder, 1 + leftSubTreeSize, n);
    // 左子树的后序遍历
    int[] leftSubTreePostorder = Arrays.copyOfRange(postorder, 0, leftSubTreeSize);
    // 右子树的后序遍历
    int[] rightSubTreePostorder = Arrays.copyOfRange(postorder, leftSubTreeSize, n - 1);
    return new TreeNode(root, buildTree(leftSubTreeInorder, leftSubTreePostorder), buildTree(rightSubTreeInorder, rightSubTreePostorder));
}