并查集的概念
并查集(Disjoint Set Union,简称 DSU,也称为 Union-Find)一种用于管理元素所属集合的数据结构,实现为一个森林,其中每棵树表示一个集合,树中的节点表示对应集合中的元素。用于处理一些不相交集合的合并及查询问题(即所谓的并、查)。它支持两种操作:
- 查找(Find):确定某个元素属于哪个集合。
- 合并(Union):将两个不相交的集合合并为一个集合。
并查集的应用
并查集主要应用于以下场景:
- 动态连通性问题:如网络连接问题,检测某些元素是否在同一个集合中。
- 最小生成树:如 Kruskal 算法。
- 图论中的连通分量:检测图中的连通分量。
并查集的java实现
用数组实现的并查集
int[] parent:- 用于存储每个元素的父节点。
- 如果元素是集合的根节点,则其父节点为自身。
int[] rank:- 用于存储每个集合的秩,即树的高度。
- 秩的作用是帮助我们在合并时保持树的平衡,从而减少查找的时间复杂度。
public UnionFind(int n):- 构造函数,初始化并查集,
n是元素数量。 - 初始状态下,每个元素的父节点是其自身,秩为1。
- 构造函数,初始化并查集,
public int find(int x):- 查找元素
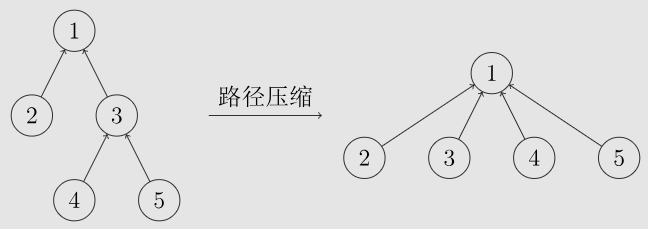
x所属集合的代表元素(根节点)。 - 使用路径压缩优化查找过程,将沿途节点直接连接到根节点。
- 查找元素
public void union(int x, int y):- 合并两个元素
x和y所在的集合。 - 使用按秩合并,将秩较小的树连接到秩较大的树上,从而保持树的平衡。
- 合并两个元素
public class UnionFind {
// 存储每个元素的父节点
private int[] parent;
// 存储每个集合的秩(树的高度)
private int[] rank;
// 初始化并查集,n是元素数量
public UnionFind(int n) {
parent = new int[n];
rank = new int[n];
for (int i = 0; i < n; i++) {
// 每个元素的父节点初始为自身
parent[i] = i;
// 每个元素的初始秩为1
rank[i] = 1;
}
}
// 查找操作,返回元素x的根节点,并进行路径压缩
public int find(int x) {
if (parent[x] != x) {
// 路径压缩,将x的父节点更新为根节点
parent[x] = find(parent[x]);
}
return parent[x];
}
// 合并操作,将两个元素x和y所在的集合合并
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
if (rank[rootX] > rank[rootY]) {
parent[rootY] = rootX;
} else if (rank[rootX] < rank[rootY]) {
parent[rootX] = rootY;
} else {
// 秩相同,任选一个作为根节点
parent[rootY] = rootX;
// 增加新根节点的秩
rank[rootX]++;
}
}
}
// 示例使用
public static void main(String[] args) {
UnionFind uf = new UnionFind(10);
uf.union(1, 2);
uf.union(2, 3);
uf.union(4, 5);
// 输出: 1
System.out.println(uf.find(1));
// 输出: 1
System.out.println(uf.find(2));
// 输出: 1
System.out.println(uf.find(3));
// 输出: 4
System.out.println(uf.find(4));
// 输出: 4
System.out.println(uf.find(5));
uf.union(3, 4);
// 输出: 1
System.out.println(uf.find(1));
// 输出: 1
System.out.println(uf.find(5));
}
}用哈希表实现的并查集
Map<T, T> parent:- 用于存储每个元素的父节点。
- 如果元素是集合的根节点,则其父节点为自身。
Map<T, Integer> rank:- 用于存储每个集合的秩,即树的高度。
- 秩的作用是帮助我们在合并时保持树的平衡,从而减少查找的时间复杂度。
public UnionFind():- 构造函数,初始化
parent和rank。
- 构造函数,初始化
public void add(T item):- 添加新元素到并查集。
- 初始状态下,每个元素的父节点是其自身,秩为1。
public T find(T item):- 查找元素所属集合的代表元素(根节点)。
- 使用路径压缩优化查找过程,将沿途节点直接连接到根节点。

public void union(T item1, T item2):- 合并两个元素所在的集合。
- 使用按秩合并,将秩较小的树连接到秩较大的树上,从而保持树的平衡。
public class UnionFind<T> {
// parent存储每个元素的父节点,rank存储每个元素的秩(树的高度)
private Map<T, T> parent;
private Map<T, Integer> rank;
// 构造函数,初始化parent和rank
public UnionFind() {
parent = new HashMap<>();
rank = new HashMap<>();
}
// 添加新元素,初始化其父节点为自己,秩为1
public void add(T item) {
if (!parent.containsKey(item)) {
parent.put(item, item);
rank.put(item, 1);
}
}
// 查找元素所属集合的代表元素(根节点),并进行路径压缩
public T find(T item) {
if (!parent.containsKey(item)) {
throw new IllegalArgumentException("Item not found");
}
// 如果当前元素不是其自己的父节点,递归查找其父节点,并进行路径压缩
if (!parent.get(item).equals(item)) {
parent.put(item, find(parent.get(item)));
}
return parent.get(item);
}
// 合并两个元素所在的集合,使用按秩合并
public void union(T item1, T item2) {
T root1 = find(item1);
T root2 = find(item2);
// 如果两个元素的根节点不同,进行合并
if (!root1.equals(root2)) {
int rank1 = rank.get(root1);
int rank2 = rank.get(root2);
// 按秩合并,将秩小的树连接到秩大的树上
if (rank1 > rank2) {
parent.put(root2, root1);
} else if (rank1 < rank2) {
parent.put(root1, root2);
} else {
parent.put(root2, root1);
rank.put(root1, rank1 + 1);
}
}
}
// 示例使用
public static void main(String[] args) {
UnionFind<String> uf = new UnionFind<>();
uf.add("a");
uf.add("b");
uf.add("c");
uf.add("d");
// 合并a和b所在的集合
uf.union("a", "b");
// 合并b和c所在的集合
uf.union("b", "c");
// 输出: true
System.out.println(uf.find("a").equals(uf.find("c")));
// 输出: false
System.out.println(uf.find("a").equals(uf.find("d")));
}
}并查集的时间复杂度
通过路径压缩和按秩合并,并查集的单次操作(查找或合并)可以在近似常量时间内完成。具体来说,其时间复杂度接近于 O(α(n)),其中 α 是反阿克曼函数,是一个非常缓慢增长的函数。对于实际应用中的数据规模,这几乎可以看作是常数时间。

