59.螺旋矩阵 II

题目:59.螺旋矩阵 II

给你一个正整数n，生成一个包含1到n^2所有元素，且元素按顺时针顺序螺旋排列的n x n正方形矩阵matrix。

• 示例 1：

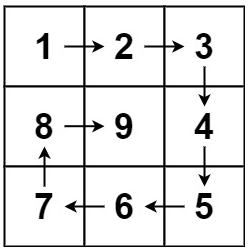
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

• 示例 2：

输入：n = 1
输出：[[1]]

• 提示：

1 <= n <= 20

思路

1. 初始化变量:
   • top 表示上边界，初始化为 0。
   • bottom 表示下边界，初始化为 matrix.length - 1。
   • left 表示左边界，初始化为 0。
   • right 表示右边界，初始化为 matrix[0].length - 1。
   • total 表示矩阵中的总元素数量。
2. 螺旋遍历:
   • 使用 while (total > 0) 循环控制遍历，当矩阵中的元素数量达到总元素数量时结束遍历。
   • 从左到右遍历顶边，并将元素添加到矩阵中，同时total-1。
   • 从上到下遍历右边，并将元素添加到矩阵中，同时total-1。
   • 从右到左遍历底边，并将元素添加到矩阵中，同时total-1。
   • 从下到上遍历左边，并将元素添加到矩阵中，同时total-1。
3. 返回结果:
   • 返回包含所有按螺旋顺序遍历的元素的矩阵。

• 时间复杂度:O(n²)
• 空间复杂度:O(n²)

代码

public int[][] generateMatrix(int n) {
    int[][] result = new int[n][n];
    int left = 0;
    int right = n - 1;
    int top = 0;
    int bottom = n - 1;
    // 矩阵中的总元素数量
    int total = n * n;
    while (total > 0) {
        // 从左到右遍历顶边
        for (int i = left; i <= right && total > 0; i++) {
            result[top][i] = n * n + 1 - total;
            total--;
        }
        // 向下移动顶边界
        top++;
        // 从上到下遍历右边
        for (int i = top; i <= bottom && total > 0; i++) {
            result[i][right] = n * n + 1 - total;
            total--;
        }
        // 向左移动右边界
        right--;
        // 从右到左遍历底边
        for (int i = right; i >= left && total > 0; i--) {
            result[bottom][i] = n * n + 1 - total;
            total--;
        }
        // 向上移动底边界
        bottom--;
        // 从下到上遍历左边
        for (int i = bottom; i >= top && total > 0; i--) {
            result[i][left] = n * n + 1 - total;
            total--;
        }
        // 向右移动左边界
        left++;
    }
    return result;
}