动态规划

能用动态规划解决的问题

动态规划在寻找有很多重叠子问题的情况的最佳解时有效。它将问题重新组合成子问题。为了避免多次解决这些子问题，它们的结果都逐渐被计算并被储存，从简单的问题直到整个问题都被解决。因此，动态规划储存递迴时的结果，因而不会在解决同样的问题时花费时间。
动态规划只能应用于有最佳子结构的问题。最佳子结构的意思是局部最佳解能决定全域最佳解（对有些问题这个要求并不能完全满足，故有时需要引入一定的近似）。简单地说，问题能够分解成子问题来解决。

如果一个问题满足以下两点，那么它就能用动态规划解决。

1. 问题的答案依赖于问题的规模​，也就是问题的所有答案构成了一个数列。举个简单的例子，1个人有2条腿，2个人有4条腿，…，n个人有多少条腿？答案是2n条腿。这里的2n是问题的答案，n则是问题的规模，显然问题的答案是依赖于问题的规模的。答案是因变量，问题规模是自变量。因此，问题在所有规模下的答案可以构成一个数列​(f(1),f(2),...f(n))，比如刚刚“数腿”的例子就构成了间隔为2的等差数列(0,2,4,...,2n)​。
2. 大规模问题的答案可以由小规模问题的答案递推得到，也就是​f(n)的值可以由​中的{f(i)|i < n}个别求得。还是刚刚“数腿”的例子，显然f(n)可以基于f(n - 1)​求得：f(n) = f(n - 1) + 2​。

适合用动态规划解决的问题

能用动态规划解决，不代表适合用。比如刚刚的“数腿”例子，你可以写成f(n) = 2n的显式表达式形式，那么杀鸡就不必用牛刀了。但是，在许多场景，f(n)的显式式子是不易得到的，大多数情况下甚至无法得到，动态规划的魅力就出来了。

应用动态规划——将动态规划拆分成三个子目标

当要应用动态规划来解决问题时，归根结底就是想办法完成以下三个关键目标。

1. 建立状态转移方程
   这一步是最难的，大部分人都被卡在这里。这一步没太多的规律可说，只需抓住一个思维：当做已经知道f(1)~f(n - 1)​的值，然后想办法利用它们求得f(n)​。在“数腿”的例子中，状态转移方程即为​f(n) = f(n - 1) + 2。
2. 缓存并复用以往结果
   这一步不难，但是很重要。如果没有合适地处理，很有可能就是指数和线性时间复杂度的区别。假设在“数腿”的例子中，我们不能用显式方程，只能用状态转移方程来解。如果现在f(100)未知，但是刚刚求解过一次f(99)​。如果不将其缓存起来，那么求f(100)时，我们就必须花100次加法运算重新获取。但是如果刚刚缓存过，只需复用这个子结果，那么将只需一次加法运算即可。
3. 按顺序从小往大算
   这里的“小”和“大”对应的是问题的规模，在这里也就是我们要从f(0)​,f(1)​,...到​f(n)依次顺序计算。这一点在“数腿”的例子来看，似乎显而易见，因为状态方程基本限制了你只能从小到大一步步递推出最终的结果（假设我们仍然不能用显式方程）。然而当问题复杂起来的时候，你有可能乱了套，所以必须记住这也是目标之一。

高中数列题的魔改版

看到这里，你可能会觉得怎么跟高中的数列题那么像？其实在我看来这就是高中数列题的魔改版。

高中的题一般需先推导出状态转移方程，再据此推导出显式表达式（在高中时代称为通项公式）。然而，动态规划是要我们在推导出状态转移方程后，根据状态转移方程用计算机暴力求解出来。显式表达式？在动态规划中是不存在的！

就是因为要暴力计算，所以前面说的目标有两个是涉及到代码层面上：

• 缓存中间结果：也就是搞个数组之类的变量记录中间结果。
• 按顺序从小往大算：也就是搞个for循环依次计算。

例子

斐波那契数列（简单）

斐波那契数列：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233……
它遵循这样的规律：当前值为前两个值的和。那么第n个值为多少？

思路

状态转移方程：dp[i] = dp[i - 1] + dp[i - 2]

代码

private BigInteger Fibonacci(int num) {
    BigInteger[] dp = new BigInteger[num + 1]; // 用于缓存以往结果，以便复用（目标2）
    // 按顺序从小往大算（目标3）
    for (int i = 0; i <= num; i++) {
        if (i <= 1) {
            dp[i] = BigInteger.valueOf(i);
        } else {
            // 使用状态转移方程（目标1），同时复用以往结果（目标2）
            dp[i] = dp[i - 1].add(dp[i - 2]);
        }
    }
    return dp[num];
}

如上代码，针对动态规划的三个子目标，都很好地实现了（参考备注），具体为：

• 目标1，建立状态转移方程（完成）。也就是前面的dp[i] = dp[i - 1] + dp[i - 2]。
• 目标2，缓存并复用以往结果（完成）。在线性规划解法中，我们把结果缓存在dp列表，同时进行了复用。这相当于我们只需完成下图中红色部分的计算任务即可，时间复杂度瞬间降为O(n)。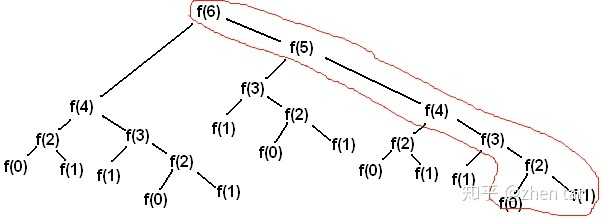
  
• 目标3，按顺序从小往大算（完成）。for循环实现了从0到​ 的顺序求解，让问题按着从小规模往大规模求解的顺序走。

面试题 08.01. 三步问题（简单）

三步问题。有个小孩正在上楼梯，楼梯有n阶台阶，小孩一次可以上1阶、2阶或3阶。实现一种方法，计算小孩有多少种上楼梯的方式。结果可能很大，你需要对结果模1000000007。

• 示例 1：

输入：n = 3 
 输出：4
 说明: 有四种走法

• 示例 2：

输入：n = 5
输出：13

• 提示：

n范围在[1, 1000000]之间

思路1

状态转移方程：dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]，因为从 i - 1、i - 2 和 i - 3 阶台阶都可以一步到达第 i 阶台阶。

• 时间复杂度:O(n)
• 空间复杂度:O(n)

代码

public int waysToStep(int n) { // 总时间复杂度：O(n)
    int[] dp = new int[n]; // 空间复杂度：O(n)
    if (n == 1) {
        return 1;
    }
    if (n == 2) {
        return 2;
    }
    if (n == 3) {
        return 4;
    }
    dp[0] = 1;
    dp[1] = 2;
    dp[2] = 4;
    for (int i = 3; i < n; i++) { // 时间复杂度：O(n)
        // 取模，对两个较大的数之和取模再对整体取模，防止越界（这里也是有讲究的）
        // 假如对三个dp[i - n]都 % 1000000007，那么也是会出现越界情况（导致溢出变为负数的问题）
        // 因为如果本来三个dp[i - n]都接近1000000007 那么取模后仍然不变，但三个相加则溢出
        // 但对两个较大的dp[i - n]: dp[i - 2],dp[i - 3]之和 mod 1000000007，那么这两个较大的数相加大于1000000007但又不溢出
        // 取模后变成一个很小的数，与dp[i - 1]相加也不溢出
        // 所以取模操作也需要仔细分析
        dp[i] = (dp[i - 2] + dp[i - 3]) % 1000000007 + dp[i - 1];
        dp[i] %= 1000000007;
    }
    return dp[n - 1];
}

思路2

优化点：考虑到结果只受三个数值的影响，这里显然不需要n维来计算，只需要3个变量d0,d1,d2即可，返回就是d2

• 时间复杂度:O(n)
• 空间复杂度:O(1)

代码

public int waysToStep(int n) { // 总时间复杂度：O(n)
    if (n == 1) {
        return 1;
    }
    if (n == 2) {
        return 2;
    }
    if (n == 3) {
        return 4;
    }
    int d0 = 1;
    int d1 = 2;
    int d2 = 4;
    for (int i = 3; i < n; i++) { // 时间复杂度：O(n)
        int t0 = d0;
        int t1 = d1;
        int t2 = d2;

        d0 = d1;
        d1 = d2;
        d2 = (t1 + t2) % 1000000007 + t0;
        d2 %= 1000000007;
    }
    return d2;
}

62.不同路径（中等）

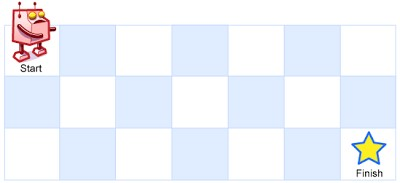
一个机器人位于一个m x n `网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

• 示例 1：

输入：m = 3, n = 7
输出：28

• 示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

• 示例 3：

输入：m = 7, n = 3
输出：28

• 示例 4：

输入：m = 3, n = 3
输出：6

思路

解这题，如前所述，我们需要完成三个子目标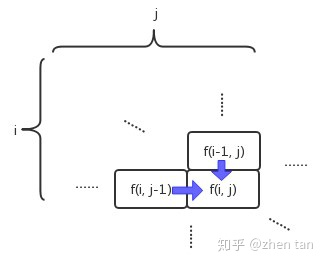

建立状态转移方程。
实际上，如上图所示，第i行第j列的格子的路径数，是等于它左边格子和上面格子的路径数之和：dp[i][j] = dp[i - 1][j] + dp[i][j - 1]​。

• 时间复杂度:O(mn)
• 空间复杂度:O(mn)

代码

public int uniquePaths(int m, int n) { // 总时间复杂度：O(mn)
    if (m == 1 || n == 1) {
        return 1;
    }
    int[][] dp = new int[m+1][n+1]; // 空间复杂度：O(mn)
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (i == 1 || j == 1) {
                dp[i][j] = 1;
            } else {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
    }
    return dp[m][n];
}

5.最长回文子串（中等）

给你一个字符串s，找到s中最长的回文子串。

• 示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

• 示例 3：

输入：s = "cbbd"
输出："bb"

• 示例 3：

输入：s = "a"
输出："a"

• 示例 4：

输入：s = "ac"
输出："a"

思路

对于一个子串而言，如果它是回文串，并且长度大于2，那么将它首尾的两个字母去除之后，它仍然是个回文串。例如对于字符串“ababa”，如果我们已经知道“bab”是回文串，那么“ababa”一定是回文串，这是因为它的首尾两个字母都是“a”。

dp[i][j]代表：[i,j]区间的string是否回文，是1否0
如下图所示，dp[2][2]代表正中间的那个"b"，dp[1][3]代表"aba"，则:

状态转移方程：dp[i][j] = dp[i + 1][j − 1] && (s[i] == s[j])

根据上图可知，可以根据左下角格子的值，依次向右上角递推。

对于完整的二维dp数组，如下图所示，我们需要将该网格右上部分填满
填充顺序:对角线->次对角线->…

  (0,0)->(1,1)->(2,2)->(3,3)->(4,4)
->(0,1)->(1,2)->(2,3)->(3,4)
->(0,2)->(1,3)->(2,4)
->(0,3)->(1,4)
->(0,4)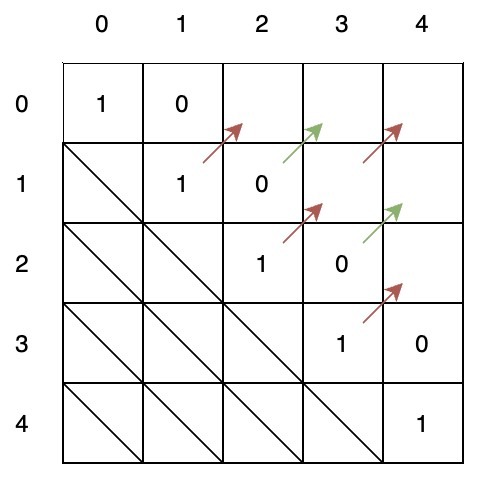

二维dp数组初始位置和边界条件: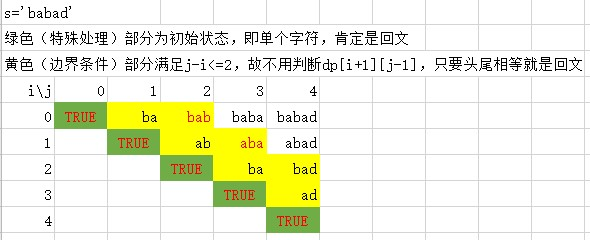

• 时间复杂度:O(n²)
• 空间复杂度:O(n²)

代码

public String longestPalindrome(String s) { // 总时间复杂度：O(n²)
    // 如果字符串长度为1,最长回文串一定是它本身
    if (s.length() == 1) {
        return s;
    }
    char[] chars = s.toCharArray();
    // 创建动态规划dynamic programing表
    boolean[][] dp = new boolean[chars.length][chars.length]; // 空间复杂度：O(n²)
    int start = 0;
    // 初始最大长度为1，这样万一不存在回文，就返回第一个值
    int maxLength = 1;
    for (int j = 1; j < dp.length; j++) {
        for (int i = 0; i < j; i++) {
            if (chars[i] == chars[j]) {
                if (j - i <= 2) {
                    dp[i][j] = true;
                } else {
                    // 状态转移方程：dp[i][j] = dp[i + 1][j − 1] && (s[i] == s[j])
                    dp[i][j] = dp[i + 1][j - 1];
                }
            } else {
                dp[i][j] = false;
            }
            // 更新最长回文子串的起始位置和最大长度
            if (dp[i][j] && j - i + 1 > maxLength) {
                start = i;
                maxLength = j - i + 1;
            }
        }
    }
    return s.substring(start, start + maxLength);
}

10.正则表达式匹配

给你一个字符串s和一个字符规律p，请你来实现一个支持'.'和'*'的正则表达式匹配。

• . 匹配任意单个字符

• * 匹配零个或多个前面的那一个元素
  所谓匹配，是要涵盖整个字符串s的，而不是部分字符串。

• 示例 1：

输入：s = "aa" p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

• 示例 2：

输入：s = "aa" p = "a*"
输出：true
解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

• 示例 3：

输入：s = "ab" p = ".*"
输出：true
解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

• 示例 4：

输入：s = "aab" p = "c*a*b"
输出：true
解释：因为 '*' 表示零个或多个，这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。

• 示例 5：

输入：s = "mississippi" p = "mis*is*p*."
输出：false

思路

我们使用我们声明一个dp[][]=new boolean[匹配串长度 + 1][模式串长度 + 1]的二位数组用来储存结果，其中dp[i][j]表示匹配串前i个和模式串前j个是否匹配。最终匹配串和模式串是否匹配就是返回dp[匹配串长度][模式串长度]。

这里的初始我们是dp[0][0]=true表示两个空串可以匹配。

我们分析这个dp[i][j]匹配串前i个，模式串前j个是否匹配.其实这个分析和之前递归还是有点相似的：

• 首先如果模式串pattern第j个如果是*，以下两种情况任意一种匹配成功即可。

1. 如果dp[i][j - 2]==true那么dp[i][j]肯定为true，因为可以把它看成一个空串。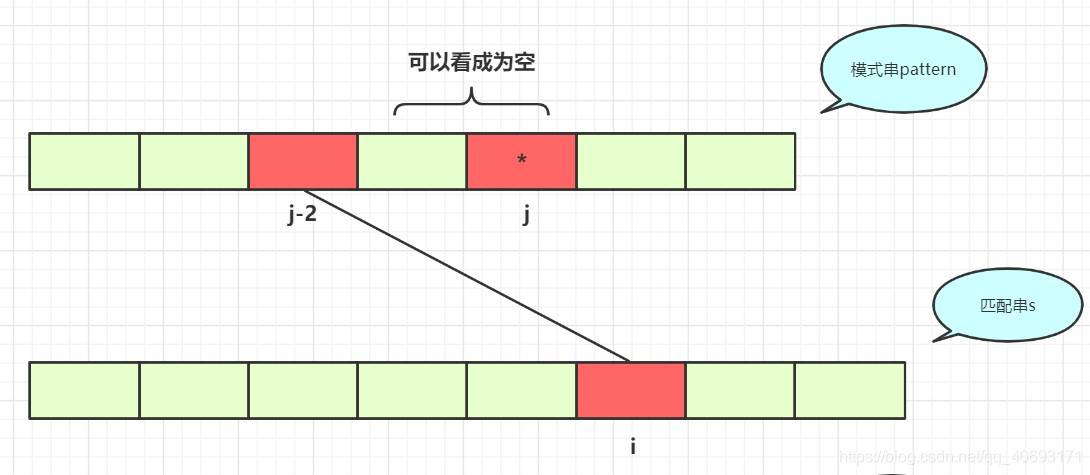
   

2. 如果匹配串和模式串前一个字符可以匹配并且dp[i - 1][j]为true，那么也可以匹配(a*和a)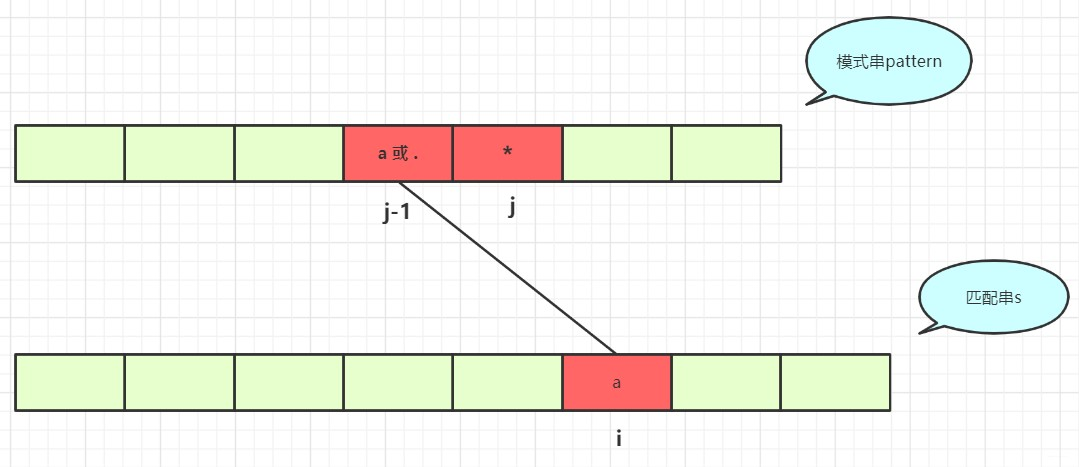
   

• 如果模式串第j个不是*那么就是常规匹配了，如果当前位置字符不匹配，那么就为false，如果当前位置匹配且dp[i - 1][j - 1]==true那么dp[i][j]就为true：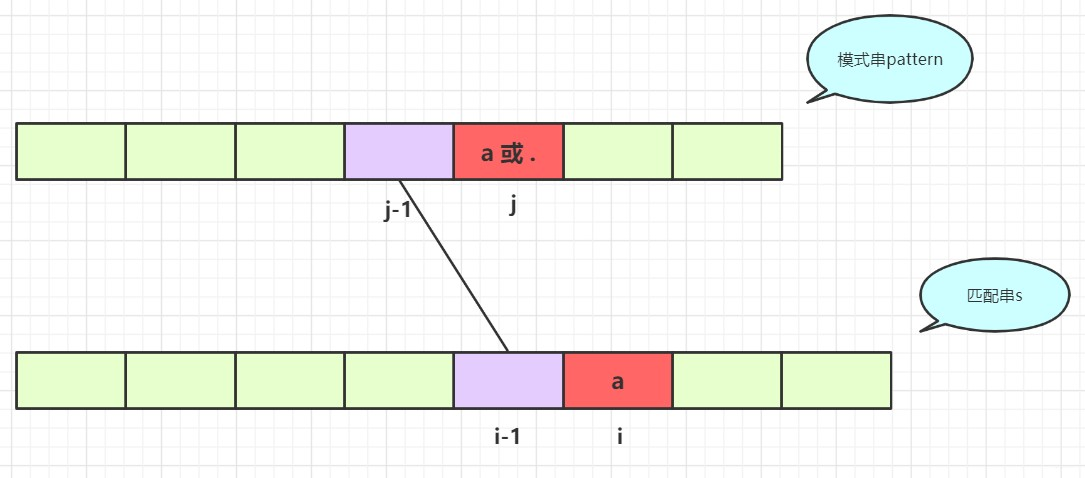
  

综上分析得到状态转移方程为：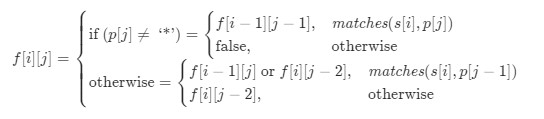

我们的dp数组的维度是 (匹配串长度 + 1) * (模式串长度 + 1)，理论上来说我们要填满所有的元素，不过为了减少循环的条件判断，我们可以对dp中第一行和第一列的数据进行单独处理。

因为dp[0][0]对应的是两个空串，可以匹配，所以dp[0][0] = true。

当i = 0，j != 0的时候s为空串，p不为空串，这时候是有可能匹配上的，比如s = ""，p = "a*"，这一行要加入循环。

当j = 0，i != 0时，s不为空，p为空，这时一定不能匹配上，可以不加入循环，否则要判断j > 0。

因为动态规划的状态转移依赖于i - 1或i - 2的状态，所以我们的循环方向是1 -> 模式串长度n。

合并上面所述，我们就可以在申请dp数组时全部初始化为false，dp[0][0]单独初始化为true，循环条件可以写成：

for (int i = 0; i <= m; ++i) {
    for (int j = 1; j <= n; ++j) {

• 时间复杂度:O(n²)
• 空间复杂度:O(n²)

代码

public boolean isMatch(String s, String p) { // 总时间复杂度：O(n²)
    int m = s.length();
    int n = p.length();
    boolean dp[][] = new boolean[m + 1][n + 1]; // 空间复杂度：O(n²)
    dp[0][0] = true; // dp[0][0]代表s和p均为空字符串，f[1][1]代表s和p的第一个字符（即在s和p中下标为0的字符
    for (int i = 0; i <= m; ++i) { // 时间复杂度：O(n²)
        for (int j = 1; j <= n; ++j) { // 时间复杂度：O(n)
            if (i > 0) {
                // p的第j个字符不为*,且s的第i个字符和p的第j个字符能匹配上
                if (p.charAt(j - 1) != '*' && (s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.')) {
                    dp[i][j] = dp[i - 1][j - 1];
                }
            }
            // p的第j个字符为*
            if (p.charAt(j - 1) == '*') {
                // p中*前面的在s中字符出现0次
                dp[i][j] = dp[i][j - 2];
                if (i > 0) {
                    // s的第i个字符和p的第j - 1个字符能匹配上
                    if (s.charAt(i - 1) == p.charAt(j - 2) || p.charAt(j - 2) == '.') {
                        // p中*前面的字符在s中出现多次或者在s中只出现1次
                        dp[i][j] = dp[i - 1][j] || dp[i][j - 2];
                    }
                }
            }
        }
    }
    return dp[m][n];
}