题目:跳跃游戏 II
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
- 示例 1:
输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。- 示例 2:
输入:[2,3,1]
输出:1- 示例 3:
输入:[10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 1, 0]
输出:[2]- 提示:
假设你总是可以到达数组的最后一个位置。思路1
贪心算法:
如果我们「贪心」地进行正向查找,每次找到可到达的最远位置,就可以在线性时间内得到最少的跳跃次数。
例如,对于数组[2,3,1,2,4,2,3],初始位置是下标0,从下标0出发,最远可到达下标2。下标0可到达的位置中,下标1的值是3,从下标1出发可以达到更远的位置,因此第一步到达下标1。
从下标1出发,最远可到达下标4。下标1可到达的位置中,下标4 的值是4,从下标4出发可以达到更远的位置,因此第二步到达下标4。
在遍历数组时,我们不访问最后一个元素,这是因为在访问最后一个元素之前,我们的边界一定大于等于最后一个位置,否则就无法跳到最后一个位置了。如果访问最后一个元素,在边界正好为最后一个位置的情况下,我们会增加一次「不必要的跳跃次数」,因此我们不必访问最后一个元素。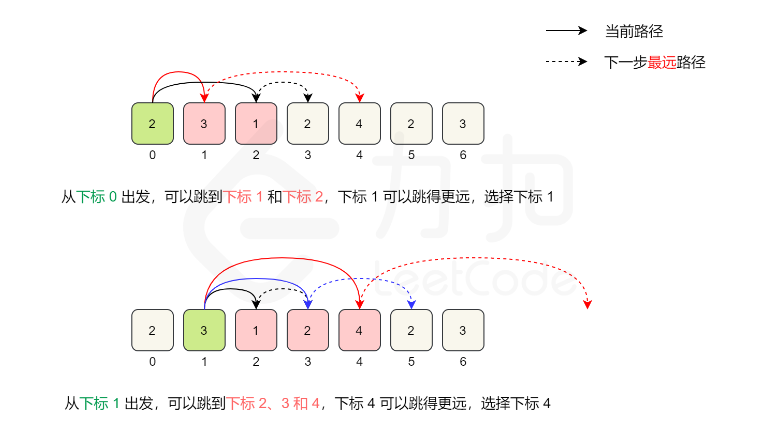
- 时间复杂度:O(n)
- 空间复杂度:O(1)
代码
public int jump(int[] nums) { // 总时间复杂度:O(n)
// 数组的长度
int length = nums.length;
// 数组的长度小于等于1时,不用跳
if (length <= 1) {
return 0;
}
// 数组的长度等于2时,可以一步到位
if (length == 2) {
return 1;
}
// curPos(currentPosition)当前位置
int curPos = 0;
// nextPos(nextPosition)下一个位置
int nextPos = 0;
// 跳跃次数
int steps = 0;
// 当前位置不在最后一个位置
while (curPos < length - 1) { // 时间复杂度:O(n)
// 这一跳能直接跳到终点,返回steps + 1
if (curPos + nums[curPos] >= length - 1) {
return steps + 1;
} else {
// 下次能跳到最远位置
int maxJump = 0;
// 对当前位置能跳到的所有位置的值做遍历,找到下次能跳到的最远位置
for (int i = 1; i <= nums[curPos]; i++) {
// 下次能跳到的位置
int jump = i + nums[curPos + i];
// 如果下次能跳到的位置是最大的
if (jump > maxJump) {
// 更新下次能跳到的最远位置
maxJump = jump;
// 更新下一个位置为能使[下次能跳到最远位置]的位置下标
nextPos = curPos + i;
}
}
// 跳跃一步
curPos = nextPos;
steps++;
}
}
return steps;
}思路2
贪心算法优化:
我们可以维护当前能够到达的最大下标位置,记为边界。我们从左到右遍历数组,到达边界时,更新边界并将跳跃次数增加1。
在遍历数组时,我们不访问最后一个元素,这是因为在访问最后一个元素之前,我们的边界一定大于等于最后一个位置,否则就无法跳到最后一个位置了。如果访问最后一个元素,在边界正好为最后一个位置的情况下,我们会增加一次「不必要的跳跃次数」,因此我们不必访问最后一个元素。
- 时间复杂度:O(n)
- 空间复杂度:O(1)
代码
public int jump(int[] nums) {
int length = nums.length;
// 跳跃次数
int steps = 0;
// 目前能跳到的最远位置
int maxPosition = 0;
// 上次跳跃可达范围右边界(下次的最右起跳点)
int end = 0;
for (int i = 0; i < length - 1; i++) {
maxPosition = Math.max(maxPosition, i + nums[i]);
// 到达上次跳跃能到达的右边界了
if (i == end) {
end = maxPosition; // 目前能跳到的最远位置变成了下次起跳位置的有边界
steps++; // 跳跃次数+1
}
}
return steps;
}
