41.缺失的第一个正数

题目:缺失的第一个正数

给你一个未排序的整数数组nums，请你找出其中没有出现的最小的正整数。

• 示例 1：

输入：nums = [1,2,0]
输出：3

• 示例 2：

输入：nums = [3,4,-1,1]
输出：2

• 示例 3：

输入：nums = [7,8,9,11,12]
输出：1

• 提示：

0 <= nums.length <= 300
-2^31 <= nums[i] <= 2^31 - 1

• 进阶：

进阶：你可以实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案吗？

思路1

哈希表（空间复杂度不符合要求）:

• 从最小的正整数1开始，依次判断2、3、4直到数组的长度N是否在数组中；

• 如果当前考虑的数不在这个数组中，我们就找到了这个缺失的最小正整数；

• 由于我们需要依次判断某一个正整数是否在这个数组里，我们可以先把这个数组中所有的元素放进哈希表。接下来再遍历的时候，就可以以O(1)的时间复杂度判断某个正整数是否在这个数组；

• 由于题目要求我们只能使用常数级别的空间，而哈希表的大小与数组的长度是线性相关的，因此空间复杂度不符合题目要求。

• 时间复杂度:O(n)

• 空间复杂度:O(n)

代码

public int firstMissingPositive(int[] nums) { // 总时间复杂度：O(n)
    // 创建一个哈希表来存放数组中所有元素
    HashSet<Integer> set = new HashSet<>(); // 空间复杂度：O(n)
    // 遍历数组,把这个数组中所有的元素放进哈希表,并求出数组中最大的元素
    for (int num : nums) { // 时间复杂度：O(n)
        set.add(num);
    }
    // 从最小的正整数1开始，依次判断2、3、4直到数组的长度nums.length是否在哈希表中,直到找到第一个不存在的元素
    for (int i = 1; i <= nums.length; i++) { // 时间复杂度：O(n)
        if (!set.contains(i)) {
            return i;
        }
    }
    // 如果都找到了,返回nums.length+1
    return nums.length + 1;
}

思路2

标记法原地哈希（哈希函数为：f(nums[i]) = nums[i] - 1）

1. 对于一个长度为N的数组，其中没有出现的最小正整数只能在[1, N+1]中。这是因为如果[1, N]都出现了，那么答案是N+1，否则答案是[1, N]中没有出现的最小正整数。这样一来，我们将所有在[1, N]范围内的数放入哈希表，也可以得到最终的答案。而给定的数组恰好长度为N，这让我们有了一种将数组设计成哈希表的思路：
2. 我们对数组进行遍历，对于遍历到的数x，如果它在[1, N]的范围内，那么就将数组中的第x−1个位置（注意：数组下标从0开始）打上「标记」。在遍历结束之后，如果所有的位置都被打上了标记，那么答案是N+1，否则答案是最小的没有打上标记的位置加1。
3. 那么如何设计这个「标记」呢？由于数组中的数没有任何限制，因此这并不是一件容易的事情。但我们可以继续利用上面的提到的性质：由于我们只在意[1, N]中的数，因此我们可以先对数组进行遍历，把不在[1, N]范围内的数修改成任意一个大于N的数（例如N+1）。这样一来，数组中的所有数就都是正数了，因此我们就可以将「标记」表示为「负号」。

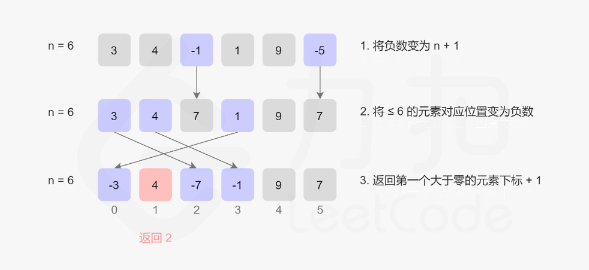
算法的流程如下：

• 我们将数组中所有小于等于0的数修改为N+1；
• 我们遍历数组中的每一个数x，它可能已经被打了标记，因此原本对应的数为|x|，其中||为绝对值符号。
  如果|x|∈[1,N]，那么我们给数组中的第|x| - 1个位置的数添加一个负号。(注意:如果它已经有负号，不需要重复添加)
• 在遍历完成之后，如果数组中的每一个数都是负数，那么答案是N+1，否则答案是第一个正数的位置加1

• 时间复杂度:O(n)
• 空间复杂度:O(1)

代码

public int firstMissingPositive(int[] nums) {
    // 数组的长度为length
    int length = nums.length;
    // 把所有小于等于0的数赋值为length(数组的长度) + 1
    for (int i = 0; i < length; i++) {
        if (nums[i] <= 0) {
            nums[i] = length + 1;
        }
    }
    // 标记:将小于等于length(数组的长度)的元素对应位置变为负数
    for (int i = 0; i < length; i++) {
        // 元素可能已经被打过标记,所以需要取绝对值
        int num = Math.abs(nums[i]);
        if (num <= length) {
            int index = num - 1;
            // 确保变成负数
            nums[index] = -Math.abs(nums[index]);
        }
    }
    // 返回第一个大于0的元素下标+1
    for (int i = 0; i < length; i++) {
        if (nums[i] > 0) {
            return i + 1;
        }
    }
    // 在遍历完成之后，如果数组中的每一个数都是负数，那么答案是length(数组的长度)+1
    return length+1;
}

思路3

置换法原地哈希（哈希函数为：f(nums[i]) = nums[i] - 1）
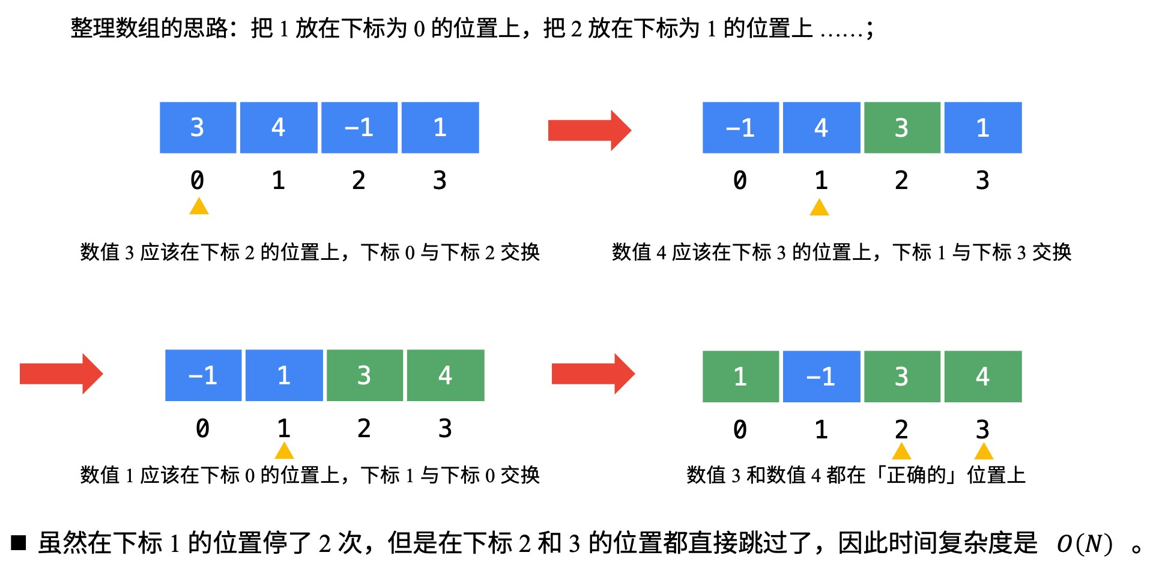
我们要找的数就在[1, N + 1]里，最后N + 1这个元素我们不用找。因为在前面的N个元素都找不到的情况下，我们才返回N + 1。
那么，我们可以采取这样的思路：就把1这个数放到下标为0的位置，2这个数放到下标为1的位置，按照这种思路整理一遍数组。然后我们再遍历一次数组，第1个遇到的它的值-1不等于下标的那个数，就是我们要找的缺失的第一个正数。
这个思想就相当于我们自己编写哈希函数，这个哈希函数的规则特别简单，那就是数值为i的数映射到下标为i - 1的位置。

• 时间复杂度:O(n)
• 空间复杂度:O(1)

代码

public int firstMissingPositive(int[] nums) {
    int length = nums.length;
    for (int i = 0; i < length; i++) {
        // 满足在指定范围内、并且没有放在正确的位置上，才交换
        while (nums[i] > 0 && nums[i] <= length && nums[nums[i] - 1] != nums[i]) {
            swap(nums, i, nums[i] - 1);
        }
    }
    // 返回第1个遇到的它的值-1不等于下标的那个数
    for (int i = 0; i < length; i++) {
        if (nums[i] - 1 != i) {
            return i + 1;
        }
    }
    // 在遍历完成之后，都正确则返回length(数组长度) + 1
    return length + 1;
}

/**
    * 方法用途:交换数组中index1索引和index2索引指向的数
    *
    * @param nums   存放要交换的数的数组
    * @param index1 第一个索引
    * @param index2 第二个索引
    **/
public void swap(int[] nums, int index1, int index2) {
    int temp = nums[index1];
    nums[index1] = nums[index2];
    nums[index2] = temp;
}