40.组合总和 II | 编程记录小站

数组回溯算法剪枝

回溯算法

发布日期: 2021-04-19

更新日期: 2024-09-29

文章字数: 1.6k

阅读时长: 6 分

题目:组合总和 II

给定一个数组candidates和一个目标数target，找出candidates中所有可以使数字和为target的组合。

candidates中的每个数字在每个组合中只能使用一次。
说明：

所有数字（包括目标数）都是正整数。
解集不能包含重复的组合。
示例 1：

输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

示例 2：

输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
  [1,2,2],
  [5]
]

提示：

1 <= candidates.length <= 30
1 <= candidates[i] <= 200
1 <= target <= 500

思路1

使用used数组加begin变量剪枝。

时间复杂度:O(2^n x n),其中n是数组candidates的长度。
空间复杂度:O(n)

代码

public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    // 排序是剪枝的前提
    Arrays.sort(candidates);
    List<List<Integer>> result = new ArrayList<>();
    // 从根结点到叶子结点的路径，是一个栈
    LinkedList<Integer> path = new LinkedList<>();
    boolean[] used = new boolean[candidates.length];
    dfs(0, used, candidates, result, path, target);
    return result;
}
/**
* 回溯算法
* @param begin      搜索起点
* @param used       状态变量
* @param candidates 候选数组
* @param target     每减去一个元素，目标值变小
* @param path       从根结点到叶子结点的路径，是一个栈
* @param result     结果集列表
**/
private void dfs(int begin, boolean[] used, int[] candidates, List<List<Integer>> result, LinkedList<Integer> path, int target) {
    // 由于进入更深层的时候，小于 0 的部分被剪枝，因此递归终止条件值只判断等于 0 的情况
    if (target == 0) {
        result.add(new LinkedList<>(path));
        return;
    }
    // 在非叶子结点处，产生不同的分支。
    // 这一操作的语义是：在还未选择的数中依次选择一个元素作为下一个位置的元素，这显然得通过一个循环实现。
    for (int i = begin; i < candidates.length; i++) {
        // 重点理解这里剪枝，前提是候选数组已经有序，如果target减去一个数得到负数，那么减去一个更大的树依然是负数。
        if (target - candidates[i] < 0) {
            break;
        }
        // 如果要搜索的数也和上一次一样且上一次的数没有被使用过,减去该分支
        if (i > 0 && candidates[i - 1] == candidates[i] && !used[i - 1]) {
            continue;
        }
        if (!used[i]) {
//            System.out.println("递归之前 => " + i + "  " + path + "，剩余 = " + (target - candidates[i]));
            used[i] = true;
            path.add(candidates[i]);
            dfs(i, used, candidates, result, path, target - candidates[i]);
//            System.out.println("递归之后 => " + i + "  " + path + "，剩余 = " + (target - candidates[i]));
            path.removeLast();
            used[i] = false;
        }
    }
}

思路2

按顺序搜索，设置合理的变量，在搜索的过程中判断是否会出现重复集结果。重点理解对输入数组排序的作用和参考代码中大剪枝和小剪枝的意思。
如何去掉重复的集合:不重复就需要按顺序搜索，在搜索的过程中检测分支是否会出现重复结果。
注意：这里的顺序不仅仅指数组candidates有序，还指按照一定顺序搜索结果。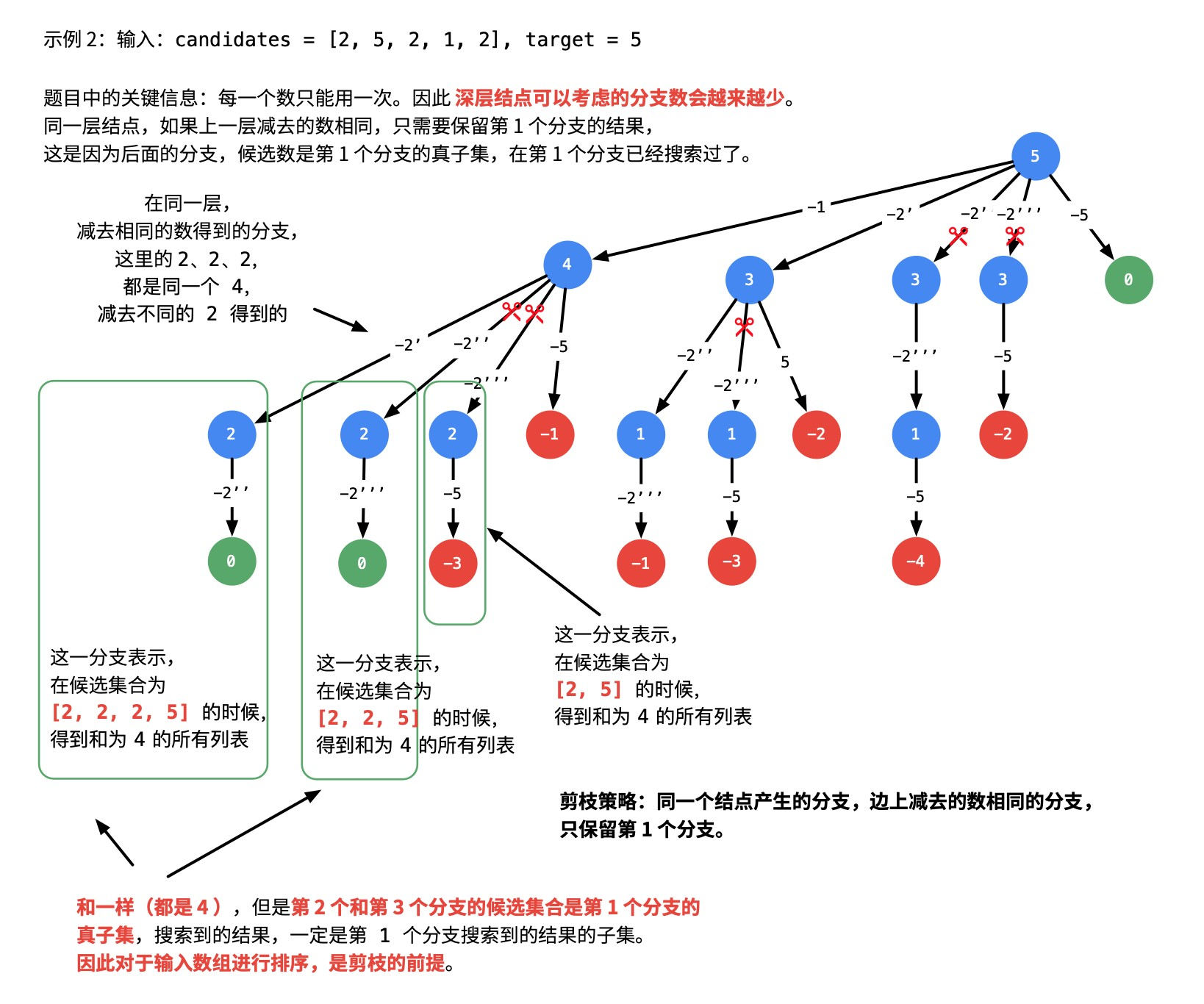
由第39题我们知道，数组candidates有序，也是深度优先遍历过程中实现「剪枝」的前提。
将数组先排序的思路来自于这个问题：去掉一个数组中重复的元素。
很容易想到的方案是：先对数组升序排序，重复的元素一定不是排好序以后相同的连续数组区域的第1个元素。
也就是说，剪枝发生在：同一层数值相同的结点第2、3 ...个结点，因为数值相同的第1个结点已经搜索出了包含了这个数值的全部结果，同一层的其它结点，候选数的个数更少，搜索出的结果一定不会比第1个结点更多，并且是第1个结点的子集。
这个方法最重要的作用是:
可以让同一层级，不出现相同的元素,即:

这种情况不会发生。

但是却允许了不同层级之间的重复,即:

这种情况可以发生。

为何会有这种神奇的效果呢？
首先candidates[i] == candidates[i - 1]是用于判定当前元素是否和之前元素相同的语句。这个语句就能砍掉例1。可是问题来了，如果把所有当前与之前一个元素相同的都砍掉，那么例2的情况也会消失。因为当第二个2出现的时候，他就和前一个2相同了。那么如何保留例2呢？
那么就用i > begin来避免这种情况，你发现例1中的两个2是处在同一个层级上的，例2的两个2是处在不同层级上的。在一个for循环中，所有被遍历到的数都是属于一个层级的。我们要让一个层级中，必须出现且只出现一个2，那么就放过第一个出现重复的2，但不放过后面出现的2。
第一个出现的2的特点就是i == begin. 第二个出现的2特点是i > begin.

代码

public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    // 排序是剪枝的前提
    Arrays.sort(candidates);
    List<List<Integer>> result = new ArrayList<>();
    // 从根结点到叶子结点的路径，是一个栈
    LinkedList<Integer> path = new LinkedList<>();
    dfs(0, candidates, result, path, target);
    return result;
}
/**
* 回溯算法
* @param begin      搜索起点
* @param candidates 候选数组
* @param target     每减去一个元素，目标值变小
* @param path       从根结点到叶子结点的路径，是一个栈
* @param result     结果集列表
**/
private void dfs(int begin, int[] candidates, List<List<Integer>> result, LinkedList<Integer> path, int target) {
    // 由于进入更深层的时候，小于 0 的部分被剪枝，因此递归终止条件值只判断等于 0 的情况
    if (target == 0) {
        result.add(new LinkedList<>(path));
        return;
    }
    for (int i = begin; i < candidates.length; i++) {
        // 大剪枝：如果target减去一个数得到负数，那么减去一个更大的树依然是负数。
        if (target - candidates[i] < 0) {
            break;
        }
        // 小剪枝：同一层相同数值的结点，从第2个开始，候选数更少，结果一定发生重复，因此跳过，用continue
        if (i > begin && candidates[i] == candidates[i - 1]) {
            continue;
        }
//            System.out.println("递归之前 => " + i + "  " + path + "，剩余 = " + (target - candidates[i]));
        path.add(candidates[i]);
        dfs(i + 1, candidates, result, path, target - candidates[i]);
//            System.out.println("递归之后 => " + i + "  " + path + "，剩余 = " + (target - candidates[i]));
        path.removeLast();
    }
}