47.全排列 II

题目:全排列 II

给定一个可包含重复数字的序列nums，按任意顺序返回所有不重复的全排列。

• 示例 1：

输入：nums = [1,1,2]
输出：
[
    [1,1,2],
    [1,2,1],
    [2,1,1]
]

• 示例 2：

输入：nums = [1,2,3]
输出：
[
    [1,2,3],
    [1,3,2],
    [2,1,3],
    [2,3,1],
    [3,1,2],
    [3,2,1]
]

思路1

回溯算法+HashSet:
先使用回溯算法求出数组全排列,然后使用一个HashSet保存所有可能的全排列,实现去重效果。但是时间复杂度比较高,可以进一步优化。

• 时间复杂度:O(n×n!)
• 空间复杂度:O(n×n!)

代码

public List<List<Integer>> permuteUnique(int[] nums) { // 总时间复杂度O(n×n!)
    // 使用一个HashSet保存所有可能的全排列,实现去重效果
    HashSet<List<Integer>> result = new HashSet<>(); // 空间复杂度O(n)
    LinkedList<Integer> path = new LinkedList<>();
    boolean[] used = new boolean[nums.length];
    dfs(nums, used, result, path); // 时间复杂度O(n×n!)
    return new ArrayList<>(result);
}

/**
* 回溯算法
*
* @param nums   候选数组
* @param used   状态变量
* @param result 结果集列表
* @param path   从根结点到叶子结点的路径，是一个栈
**/
private void dfs(int[] nums, boolean[] used, Set<List<Integer>> result, LinkedList<Integer> path) {
    // 递归出口,当路径长度等于数组长度时,将此路径添加到结果集中,返回
    if (path.size() == nums.length) {
        result.add(new LinkedList<>(path));
        return;
    }
    // 在非叶子结点处，产生不同的分支。
    // 这一操作的语义是：在还未选择的数中依次选择一个元素作为下一个位置的元素，这显然得通过一个循环实现。
    for (int i = 0; i < nums.length; i++) {
        if (!used[i]) {
            path.add(nums[i]);
            used[i] = true;
//            System.out.println("递归之前 => " + i + "  " + path);
            dfs(nums, used, result, path);
            // 注意：下面这两行代码发生「回溯」，回溯发生在从深层结点回到浅层结点的过程，代码在形式上和递归之前是对称的
            used[i] = false;
//            System.out.println("递归之后 => " + i + "  " + path);
            path.removeLast();
        }
    }
}

思路2

回溯算法+剪枝:
在遍历的过程中，一边遍历一遍检测，在一定会产生重复结果集的地方剪枝。
如果要比较两个列表是否一样，一个容易想到的办法是对列表分别排序，然后逐个比对。既然要排序，我们就可以在搜索之前就对候选数组排序，一旦发现某个分支搜索下去可能搜索到重复的元素就停止搜索，这样结果集中不会包含重复列表。

画出树形结构如下：重点想象深度优先遍历在这棵树上执行的过程，哪些地方遍历下去一定会产生重复，这些地方的状态的特点是什么？
对比图中标注①和②的地方。相同点是：这一次搜索的起点和上一次搜索的起点一样。不同点是：

• 标注①的地方上一次搜索的相同的数刚刚被撤销；
• 标注②的地方上一次搜索的相同的数刚刚被使用。

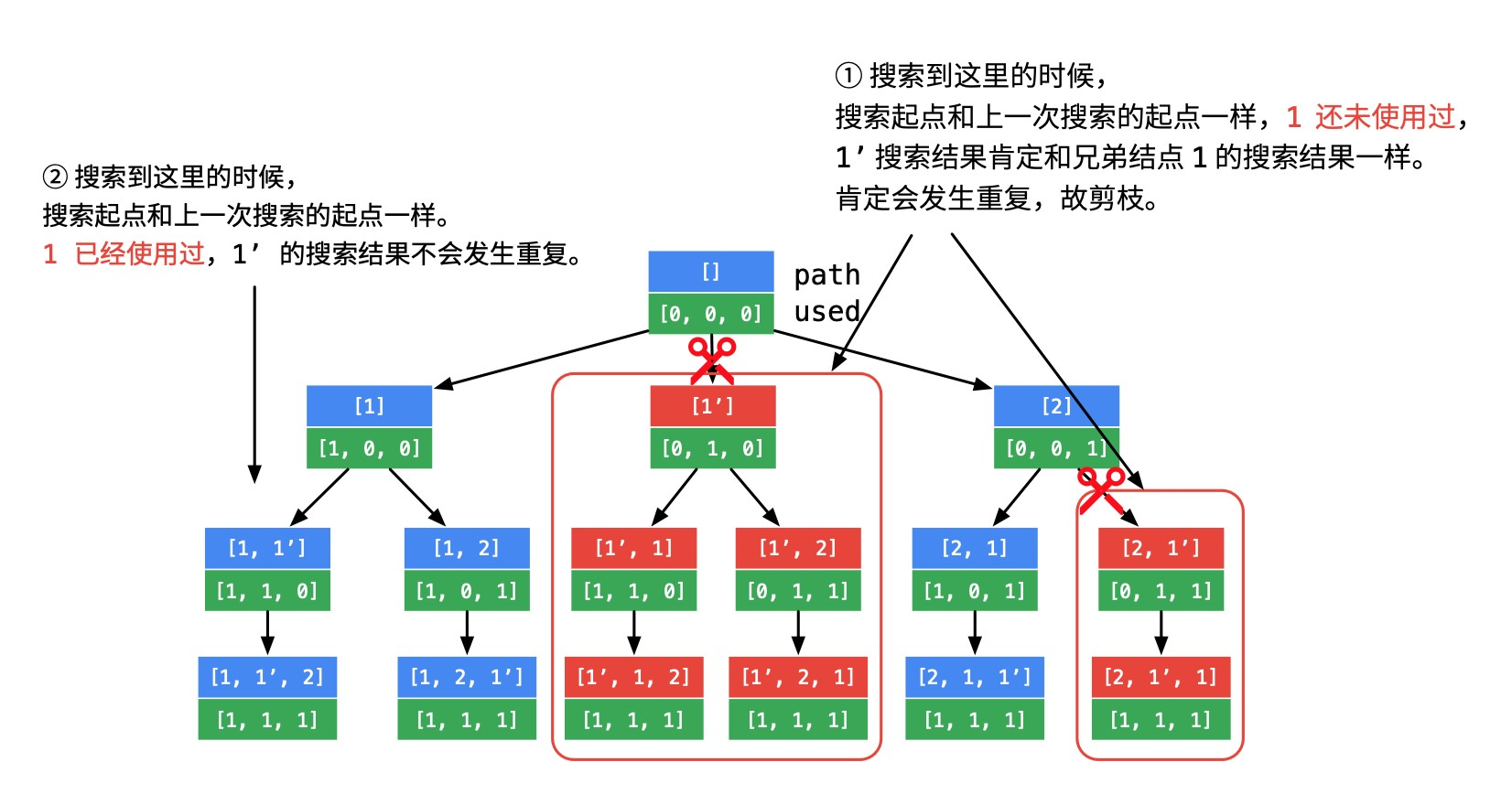
产生重复结点的地方，正是图中标注了「剪刀」，且被绿色框框住的地方。
把第2个1加上'，即[1, 1', 2]去想象这个搜索的过程。只要遇到起点一样，就有可能产生重复。这里还有一个很细节的地方：

• 在图中②处，搜索的数也和上一次一样，但是上一次的1还在使用中；
• 在图中①处，搜索的数也和上一次一样，但是上一次的1刚刚被撤销，正是因为刚被撤销，下面的搜索中还会使用到，因此会产生重复，剪掉的就应该是这样的分支。

代码实现方面，在第 46 题的基础上，要加上这样一段代码：

if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
    continue;
}

这段代码就能检测到标注为①的两个结点，跳过它们。

• 时间复杂度:O(n × n!)
• 空间复杂度:O(n × n!)

代码

public List<List<Integer>> permuteUnique(int[] nums) { // 总时间复杂度O(n×n!)
    // 排序是剪枝的前提
    Arrays.sort(nums);
    // 使用一个动态数组保存所有可能的全排列
    List<List<Integer>> result = new ArrayList<>();
    // path表示路径
    LinkedList<Integer> path = new LinkedList<>();
    // 布尔数组used作为状态变量判断这个数是否被选择过
    boolean[] used = new boolean[nums.length];
    dfs(nums, used, result, path); // 时间复杂度O(n×n!)
    return new ArrayList<>(result);
}

/**
* 回溯算法
*
* @param nums   候选数组
* @param used   状态变量
* @param result 结果集列表
* @param path   从根结点到叶子结点的路径，是一个栈
**/
private void dfs(int[] nums, boolean[] used, List<List<Integer>> result, LinkedList<Integer> path) {
    // 递归出口,当路径长度等于数组长度时,将此路径添加到结果集中,返回
    if (path.size() == nums.length) {
        result.add(new LinkedList<>(path));
        return;
    }
    // 在非叶子结点处，产生不同的分支。
    // 这一操作的语义是：在还未选择的数中依次选择一个元素作为下一个位置的元素，这显然得通过一个循环实现。
    for (int i = 0; i < nums.length; i++) {
        // 如果要搜索的数也和上一次一样且上一次的数没有被使用过,减去该分支
        if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
            continue;
        }
        if (!used[i]) {
            path.add(nums[i]);
            used[i] = true;
//            System.out.println("回溯前路径" + path);
            dfs(nums, used, result, path);
            // 注意：下面这两行代码发生「回溯」，回溯发生在从深层结点回到浅层结点的过程，代码在形式上和递归之前是对称的
            used[i] = false;
//            System.out.println("回溯后路径" + path);
            path.removeLast();
        }
    }
}