46.全排列

题目:全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

• 示例 1：

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

思路

使用回溯算法:

1. 总结搜索全排列的方法：按顺序枚举每一位可能出现的情况，已经选择的数字在当前要选择的数字中不能出现。按照这种策略搜索就能够做到不重不漏。这样的思路，可以用一个树形结构表示。
   

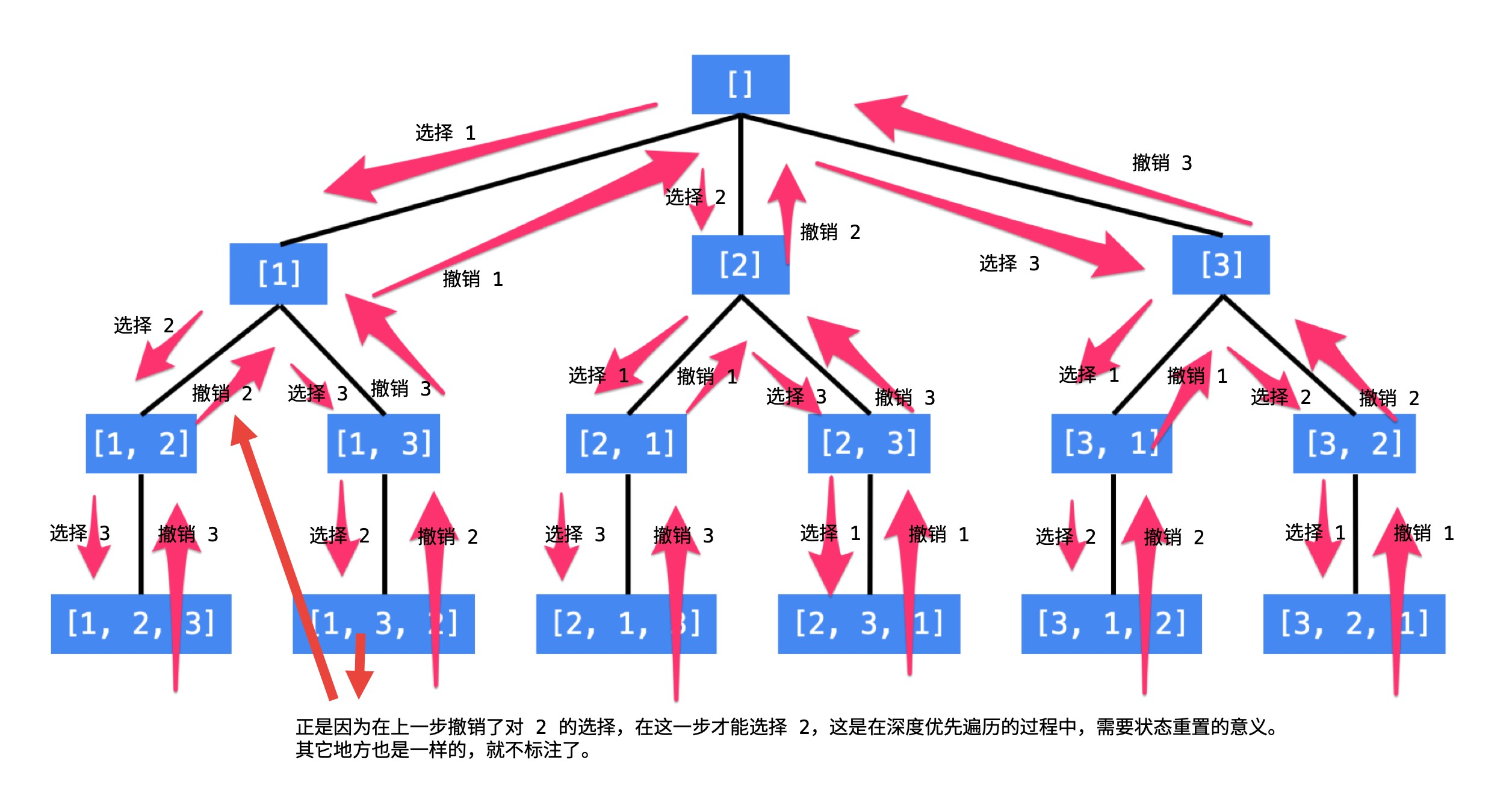
2. 说明：每一个结点表示了求解全排列问题的不同的阶段，这些阶段通过变量的「不同的值」体现，这些变量的不同的值，称之为「状态」；
   使用深度优先遍历有「回头」的过程，在「回头」以后，状态变量需要设置成为和先前一样，因此在回到上一层结点的过程中，需要撤销上一次的选择，这个操作称之为「状态重置」；
   深度优先遍历，借助系统栈空间，保存所需要的状态变量，在编码中只需要注意遍历到相应的结点的时候，状态变量的值是正确的，具体的做法是：往下走一层的时候，path变量在尾部追加，而往回走的时候，需要撤销上一次的选择，也是在尾部操作，因此path变量是一个栈；
   深度优先遍历通过「回溯」操作，实现了全局使用一份状态变量的效果。
   使用编程的方法得到全排列，就是在这样的一个树形结构中完成遍历，从树的根结点到叶子结点形成的路径就是其中一个全排列。

3. 设计状态变量:布尔数组used，初始化的时候都为false表示这些数还没有被选择，当我们选定一个数的时候，就将这个数组的相应位置设置为true，这样在考虑下一个位置的时候，就能够以O(1)的时间复杂度判断这个数是否被选择过，这是一种「以空间换时间」的思想。

• 时间复杂度:O(n × n!)
• 空间复杂度:O(n × n!)

代码

public List<List<Integer>> permute(int[] nums) { // 总时间复杂度O(n×n!)
    // 使用一个动态数组保存所有可能的全排列
    List<List<Integer>> result = new ArrayList<>();
    // path表示路径
    LinkedList<Integer> path = new LinkedList<>();
    // 布尔数组used作为状态变量判断这个数是否被选择过
    boolean[] used = new boolean[nums.length];
    dfs(nums, used, result, path); // 时间复杂度O(n×n!)
    return result;
}

/**
* 回溯算法
*
* @param nums   候选数组
* @param used   状态变量
* @param result 结果集列表
* @param path   从根结点到叶子结点的路径，是一个栈
**/
private void dfs(int[] nums, boolean[] used, List<List<Integer>> result, LinkedList<Integer> path) {
    // 递归出口,当路径长度等于数组长度时,将此路径添加到结果集中,返回
    if (path.size() == nums.length) {
        result.add(new LinkedList<>(path));
        return;
    }
    // 在非叶子结点处，产生不同的分支。
    // 这一操作的语义是：在还未选择的数中依次选择一个元素作为下一个位置的元素，这显然得通过一个循环实现。
    for (int i = 0; i < nums.length; i++) {
        if (!used[i]) {
            path.add(nums[i]);
            used[i] = true;
//            System.out.println("递归之前 => " + i + "  " + path);
            dfs(nums, used, result, path);
            // 注意：下面这两行代码发生「回溯」，回溯发生在从深层结点回到浅层结点的过程，代码在形式上和递归之前是对称的
            used[i] = false;
//            System.out.println("递归之后 => " + i + "  " + path);
            path.removeLast();
        }
    }
}