题目:组合总和
给定一个无重复元素的数组candidates和一个目标数target,找出candidates中所有可以使数字和为target的组合。
candidates中的数字可以无限制重复被选取。
说明:
所有数字(包括
target)都是正整数。解集不能包含重复的组合。
示例 1:
输入:candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]- 示例 2:
输入:candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]- 提示:
1 <= candidates.length <= 30
1 <= candidates[i] <= 200
candidate 中的每个元素都是独一无二的。
1 <= target <= 500思路
- 思路分析:根据示例 1:输入:
candidates = [2, 3, 6, 7],target = 7。
候选数组里有2,如果找到了组合总和为7 - 2 = 5的所有组合,再在之前加上2,就是7的所有组合;
同理考虑3,如果找到了组合总和为7 - 3 = 4的所有组合,再在之前加上3,就是7的所有组合,依次这样找下去。 - 画出树形图:以输入:
candidates = [2, 3, 6, 7],target = 7为例,基于以上的想法,可以画出如下的树形图。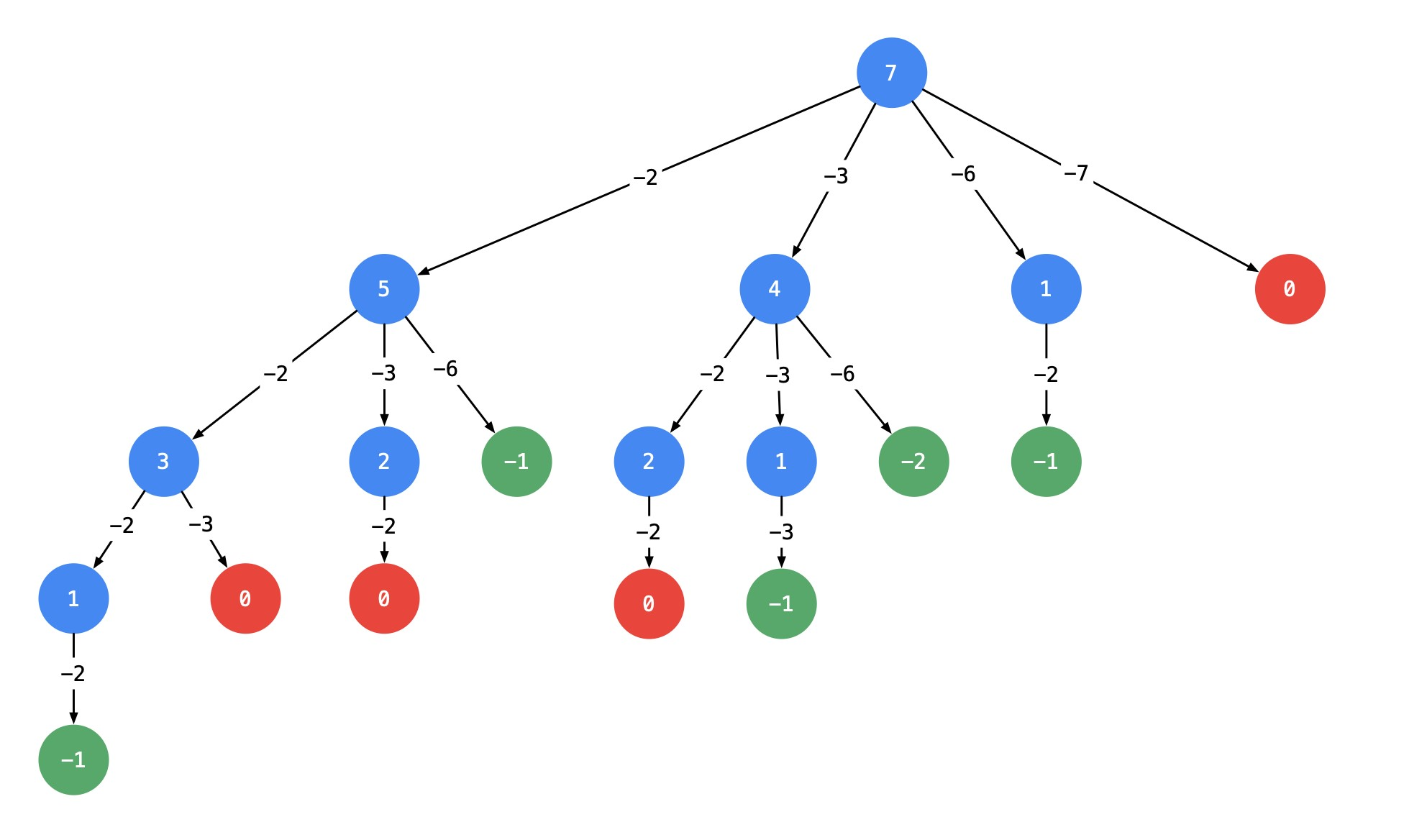
说明:
- 以
target = 7为根结点,创建一个分支的时做减法; - 每一个箭头表示:从父亲结点的数值减去边上的数值,得到孩子结点的数值。边的值就是题目中给出的
candidate数组的每个元素的值; - 减到
0或者负数的时候停止,即:结点0和负数结点成为叶子结点; - 所有从根结点到结点
0的路径(只能从上往下,没有回路)就是题目要找的一个结果。
这棵树有4个叶子结点的值0,对应的路径列表是[[2, 2, 3], [2, 3, 2], [3, 2, 2], [7]],而示例中给出的输出只有[[7], [2, 2, 3]]。
即:题目中要求每一个符合要求的解是不计算顺序的。下面我们分析为什么会产生重复。
针对具体例子分析重复路径产生的原因
产生重复的原因是:在每一个结点,做减法,展开分支的时候,由于题目中说 每一个元素可以重复使用,我们考虑了 所有的 候选数,因此出现了重复的列表。
可不可以在搜索的时候就去重呢?答案是可以的。遇到这一类相同元素不计算顺序的问题,我们在搜索的时候就需要 按某种顺序搜索。具体的做法是:每一次搜索的时候设置 下一轮搜索的起点begin,请看下图。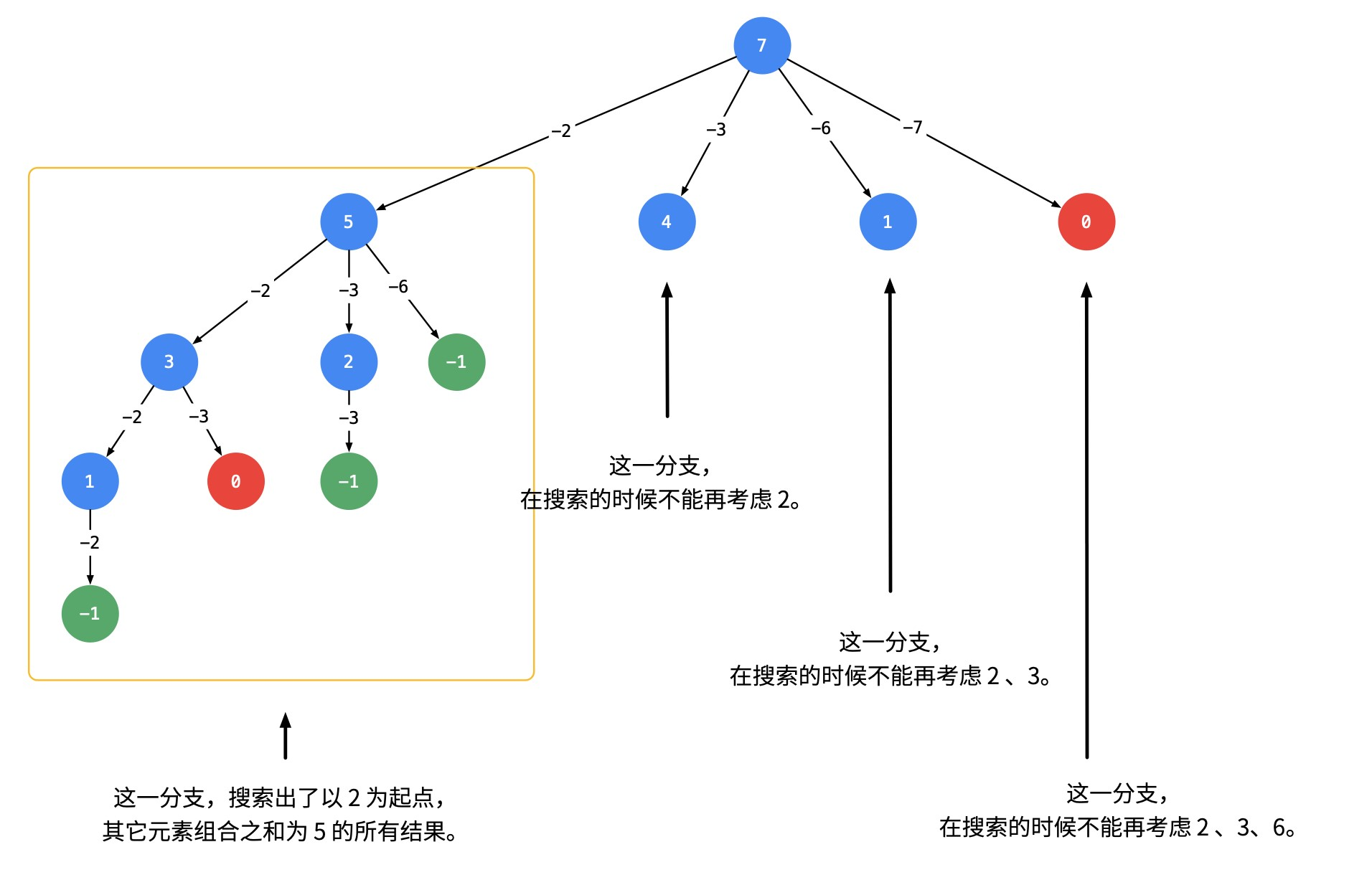
即:从每一层的第2个结点开始,都不能再搜索产生同一层结点已经使用过的candidate里的元素。什么时候使用
used数组,什么时候使用begin变量
排列问题,讲究顺序(即
[2, 2, 3]与[2, 3, 2]视为不同列表时),需要记录哪些数字已经使用过,此时用used数组;组合问题,不讲究顺序(即
[2, 2, 3]与[2, 3, 2]视为相同列表时),需要按照某种顺序搜索,此时使用begin变量。时间复杂度:
O(S),其中S为所有可行解的长度之和。从分析给出的搜索树我们可以看出时间复杂度取决于搜索树所有叶子节点的深度之和,即所有可行解的长度之和。空间复杂度:
O(target)。除答案数组外,空间复杂度取决于递归的栈深度,在最差情况下需要递归O(target)层。
代码
public List<List<Integer>> combinationSum(int[] candidates, int target) {
if (candidates.length == 0) {
return new ArrayList<>();
}
// 排序是剪枝的前提
Arrays.sort(candidates);
List<List<Integer>> result = new ArrayList<>();
// 从根结点到叶子结点的路径,是一个栈
LinkedList<Integer> path = new LinkedList<>();
dfs(0, candidates, target, path, result);
return result;
}
/**
* 回溯算法
* @param begin 搜索起点
* @param candidates 候选数组
* @param target 每减去一个元素,目标值变小
* @param path 从根结点到叶子结点的路径,是一个栈
* @param result 结果集列表
**/
private void dfs(int begin, int[] candidates, int target, LinkedList<Integer> path, List<List<Integer>> result) {
// 由于进入更深层的时候,小于 0 的部分被剪枝,因此递归终止条件值只判断等于 0 的情况
if (target == 0) {
result.add(new LinkedList<>(path));
return;
}
for (int i = begin; i < candidates.length; i++) {
// 重点理解这里剪枝,前提是候选数组已经有序,如果target减去一个数得到负数,那么减去一个更大的树依然是负数。
if (target - candidates[i] < 0) {
break;
}
// System.out.println("递归之前 => " + i + " " + path + ",剩余 = " + (target - candidates[i]));
path.add(candidates[i]);
dfs(i, candidates, target - candidates[i], path, result);
// System.out.println("递归之后 => " + i + " " + path + ",剩余 = " + (target - candidates[i]));
path.removeLast();
}
}
