31.下一个排列

题目:下一个排列

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须原地修改，只允许使用额外常数空间。

• 示例 1：

输入：nums = [1,2,3]
输出：[1,3,2]

• 示例 2：

输入：nums = [3,2,1]
输出：[1,2,3]

• 示例 3：

输入：nums = [1,1,5]
输出：[1,5,1]

• 示例 4：

输入：nums = [1]
输出：[1]

• 提示：

1 <= nums.length <= 100
0 <= nums[i] <= 100

思路

注意到下一个排列总是比当前排列要大，除非该排列已经是最大的排列。我们希望找到一种方法，能够找到一个大于当前序列的新序列，且变大的幅度尽可能小。具体地：

1. 我们需要将一个左边的「较小数」与一个右边的「较大数」交换，以能够让当前排列变大，从而得到下一个排列。
2. 同时我们要让这个「较小数」尽量靠右，而「较大数」尽可能小。当交换完成后，「较大数」右边的数需要按照升序重新排列。这样可以在保证新排列大于原来排列的情况下，使变大的幅度尽可能小。

以排列[1,5,8,4,7,6,5,3,1]为例:

• 我们能找到的符合条件的一对「较小数」与「较大数」的组合为4与5，满足「较小数」尽量靠右，而「较大数」尽可能小。
• 当我们完成交换后排列变为[1,5,8,5,7,6,4,3,1]，此时我们可以重排「较小数」右边的序列，序列变为[1,5,8,5,1,3,4,6,7]。

解法

具体地，我们这样描述该算法，对于长度为n的排列a：

1. 首先从后向前查找第一个顺序对(i,i + 1)，满足a[i] < a[i + 1]。这样「较小数」即为a[i]。此时[i + 1,n)必然是下降序列。
2. 如果找到了顺序对，那么在区间[i + 1,n)中从后向前查找第一个元素j满足a[i] < a[j]。这样「较大数」即为a[j]。
3. 交换a[i]与a[j]，此时可以证明区间[i + 1,n)必为降序。我们可以直接使用双指针反转区间[i + 1,n)使其变为升序，而无需对该区间进行排序。

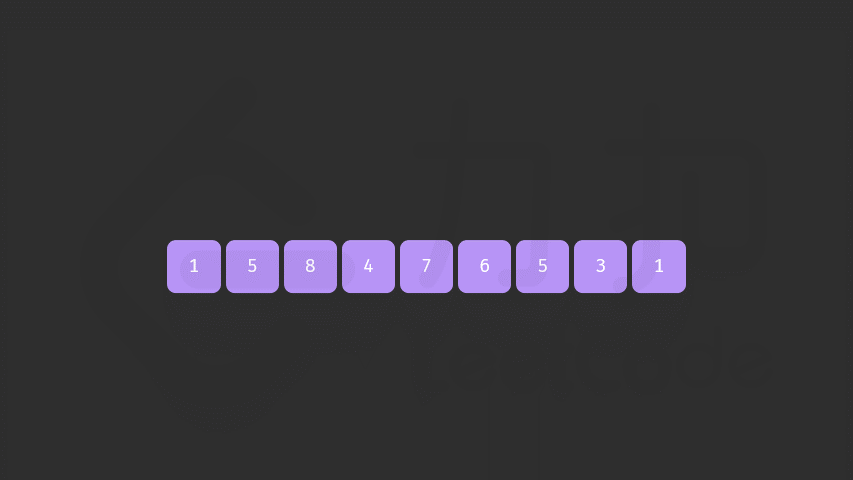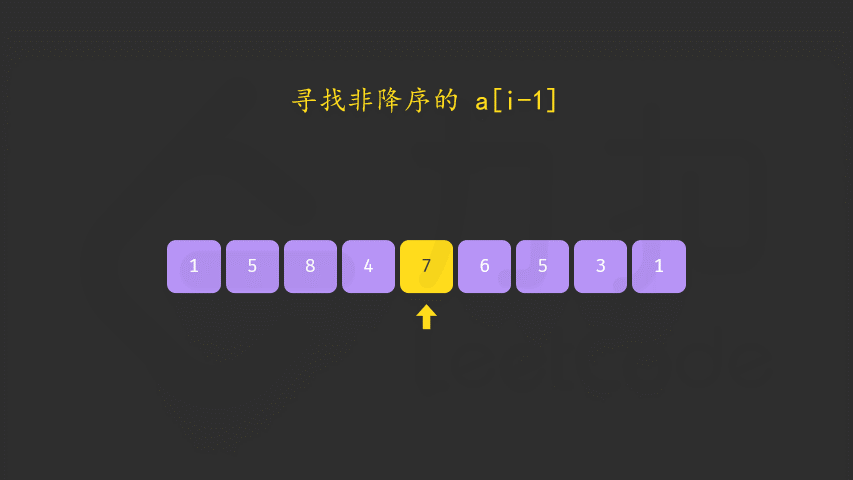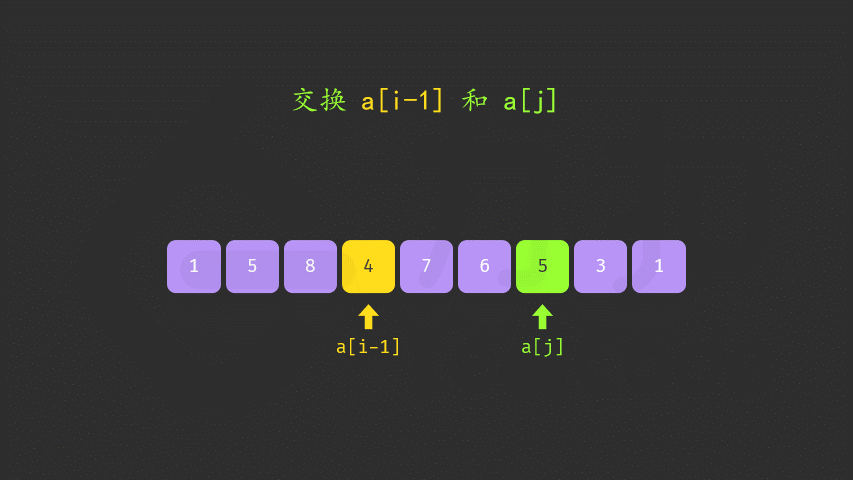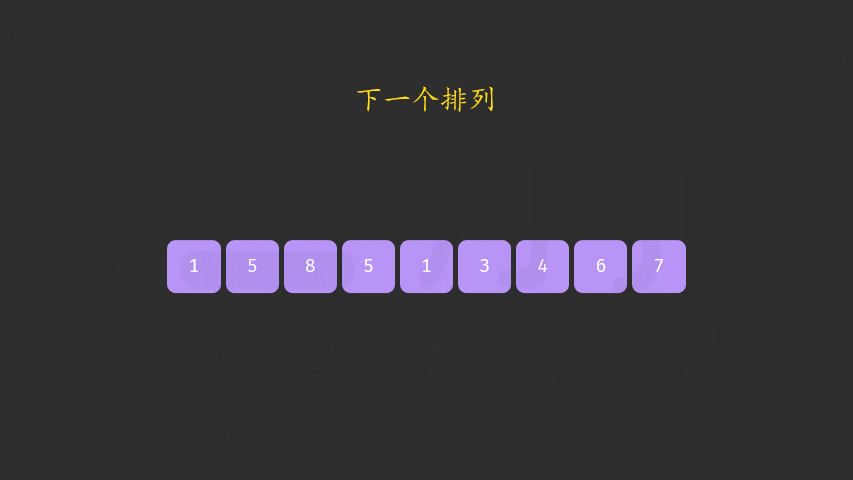
代码

public void nextPermutation(int[] nums) {
    // 在尽可能靠右的低位进行交换，需要从后向前查找
    int i = nums.length - 2;
    int j = nums.length - 1;
    // 先找出最大的索引i满足nums[i] < nums[i + 1]，如果不存在，就翻转整个数组；
    // 满足「较小数」尽量靠右
    while (i >= 0 && nums[i] >= nums[i + 1]) {
        i--;
    }
    if (i >= 0) {
        // 再找出另一个最大索引j满足nums[j] > nums[i]；
        // 「较大数」尽可能小
        while (j > i && nums[i] >= nums[j]) {
            j--;
        }
        // 交换 nums[i] 和 nums[j]；
        swap(nums, i, j);
    }
    // 最后翻转nums[i + 1]到nums[nums.length - 1]。
    reverse(nums, i + 1, nums.length - 1);
}
/**
    * 方法用途:翻转数组中begin索引到end索引之间的数
    * 参数: nums数组,begin开始索引,end结束索引
    **/
private void reverse(int[] nums, int begin, int end) {
    int left = begin;
    int right = end;
    while (left < right) {
        swap(nums, left, right);
        left++;
        right--;
    }
}

/**
    * 方法用途:交换数组中a索引和b索引指向的数
    * 参数: nums数组,a索引,b索引
    **/
private void swap(int[] nums, int a, int b) {
    int temp = nums[a];
    nums[a] = nums[b];
    nums[b] = temp;
}