867.转置矩阵

题目:转置矩阵

给你一个二维整数数组matrix， 返回matrix的转置矩阵。

矩阵的转置是指将矩阵的主对角线翻转，交换矩阵的行索引与列索引。

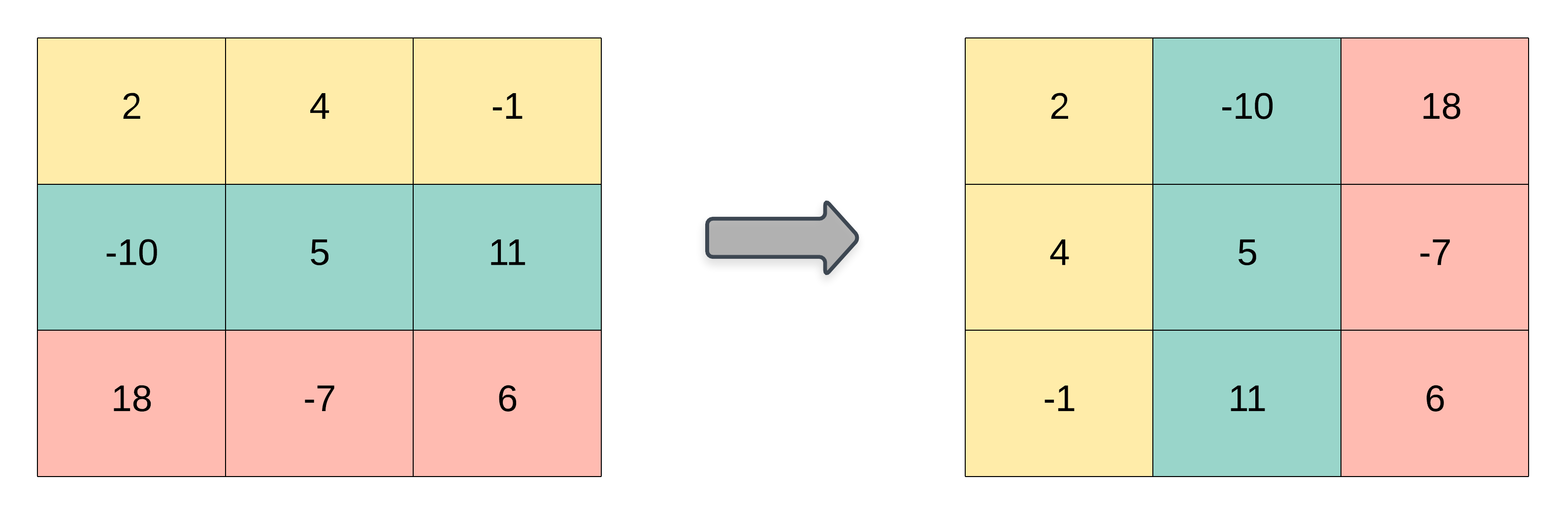
• 示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[1,4,7],[2,5,8],[3,6,9]]

• 示例 2：

输入：matrix = [[1,2,3],[4,5,6]]
输出：[[1,4],[2,5],[3,6]]

• 提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 1000
1 <= m * n <= 10^5
-10^9 <= matrix[i][j] <= 10^9

思路

正如题目给出的示例图所描述的，转置矩阵就是把MM行NN列的矩阵，转成NN行MM列的矩阵，原来矩阵中matrix[i][j]matrix[i][j]的位置，会交换到新矩阵的arr[j][i]arr[j][i]位置。

注意：本题的矩阵的行列数可能不等，因此不能做原地操作，需要新建数组。

• 时间复杂度:O(mn)
• 空间复杂度:O(mn)

代码

public int[][] transpose(int[][] matrix) { // 总时间复杂度:O(mn)
    // 新建一个数组,行数和列数分别对应原来数组的列数和行数
    int[][] arr = new int[matrix[0].length][matrix.length]; // 空间复杂度:O(mn)

    for (int i = 0; i <= matrix.length - 1; i++) {
        // 新数组j行i列上的元素为原来数组i行j列上的元素
        for (int j = 0; j <= matrix[i].length - 1; j++) {
            arr[j][i] = matrix[i][j];
        }
    }
    return arr;
}